[MATHS] Pensez-vous qu'à nous tous nous puissions résoudre la conjecture de Syracuse ?

Le 15 avril 2020 à 18:21:01 Drayon a écrit :

hérédité: supposons syracuse vérifié jusqu'à n>10^100 alors on peut faire l'approximation (3n+1)/2 = 3n/2

Ah oui on a du level sur ce topic

3n/2 est un Horizontale blue.

Le 15 avril 2020 à 18:24:06 Ghauss3 a écrit :

Le 15 avril 2020 à 18:21:01 Drayon a écrit :

hérédité: supposons syracuse vérifié jusqu'à n>10^100 alors on peut faire l'approximation (3n+1)/2 = 3n/2

Ah oui on a du level sur ce topic

3n/2 est un Horizontale blue.

Ca me paraît évident

Le 15 avril 2020 à 18:23:53 Doujinologue a écrit :

Le 15 avril 2020 à 18:22:16 Ghauss3 a écrit :

Le 15 avril 2020 à 18:15:52 Doujinologue a écrit :
Tout d'abord j'étudie la suite dans la définition [0;+inf[ sans le zéro

On sait qu'un nombre pair est divisé par 2 et qu'un nombre impair multiplié par 3 et +1

Je simplifie la suite de la manière suivante : nous ne travaillerons qu'avec la somme digitale de chaque nombre et résultat

On dresse le tableau suivant en fonction de la parité du nombre départ et de sa somme digitale
Le nombre digital parent est en gras et le nombre digital enfant est souligné

1/2 = 0,5 5
1*3+1 = 4

2/2 = 1
2*3+1 = 7

3/2 = 1,5 6
3*3+1 = 10 1

4/2 = 2
4*3+1 = 13 4

5/2 = 2,5 7
5*3+1 = 16 7

6/2 = 3
6*3+1 = 19 10 1

7/2 = 3,5 8
7*3+1 = 22 4

8/2 = 4
8*3+1 = 25 7

9/2 = 4,5 9
9*3+1 = 28 10 1

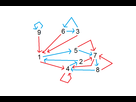
On peut dresser l'a figure suivante où grâce à ça
- Les chiffres représentent la somme digitale du nombre X
- Les flèches désignent quelle opération l'ont fait du nombre X (Flèche bleu /2) ( Flèche rouge *3+1)

Ainsi nous voyons que peu importe le nombre de départ on peut atteindre chaque étape et donc tous les nombres sont liés entre eux mais on voit 3 exceptions :

Propiété 1 : Si on ne commence pas par un nombre dont la somme digitale est de 3 6 ou 9 il sera impossible d'en avoir (représenté par les flèches à sens unique)

Proprité 2: On sait aussi que si le nombre X est impair alors le prochain calcul donnera forcément un nombre pair donc flèche rouge

Avec la Propriété2 il ne peut donc pas avoir 2 opérations impairs à la suite

Donc le nombre X aura qu'un nombre égal d'étapes et devra alterner pair et impair pour boucler, car s'il y a que des opérations pairs ou plus d'opérations pair qu'impaire, il tendra vers 1 donc la boucle 4 2 1

Il faut trouver des boucles qui boucles comme : IP , IPIP, IPIPIP etc..

Comme les 9I 6I 3I sont à sens uniques et bouclent sur du pair elles vont tendre vers 1

On doit qu'utiliser les 1I 2I 4I 5I 7I 8I 1P 2P 4P 5P 7P 8P car elle

dans une suite de + de 2 nombres ne doit pas contenir un 7P car il donnera un 8I et bouclera sur 7P8I etc

Etant la seule boucle qui alterne Pair et Impair avec 2 éléments on doit passer à des boucles de 3 éléments ou + et donc exclure 7P et 8I

Boucles possibles : 7P8I

---

Le seul moyen d'accèder à 5 est par un 1P, donc 5P n'est pas disponible

Possibilités restantes : 1I 2I 4I 5I 7I 1P 2P 4P 8P

Donc 5I mènera forcément à 7P, or ce n'est pas une boucle valable donc on supprime 5I
Si on supprime 5I et 5P il faut supprimer 1P qui était le seul chemin qui y menait

Possibilités restantes : 1I 2I 4I 7I 2P 4P 8P

Pour avoir un 8P il faut un 7P or ce n'est pas possible 2P à la suite

Possibilités restantes : 1I 2I 4I 7I 2P 4P

La suite 2I 7I n'est pas possible

Possibilités restantes : 1I 4I 2P 4P

4I ne peut pas boucler sur lui même car seul chemin venant vers 4 et 1I

Possibilités restantes : 1I 2P 4P

Nous avons donc que 2 boucles possibles

1 à 2 éléments : 7P 8I
1 à 3 éléments : 1I 2P 4P

Or selon forumeur vinsmock il est impossible d'alterner infiniment entre pair et impair

Comme une boucle pair impair est impossible le nombre diminuera forcément et donc tendra vers 4P 2P 1I

Based, descopilled et trivial

De ce que j'en ai vu, ça m'a l'air faux dès le début avec l'ensemble de travail, puis brouillon avec ton système de notation et ton schéma, ça ne mène pas à grand chose... désolé.
Surtout que là tu n'as absolument pas généralisé.

Comment ça généraliser? Fallait juste démontrer que ça tend vers 4 2 1

Et tu as donc trouvé une séquence qui ne se termine pas par le cycle éternel concrètement ?
Pas vraiment de ce que j'en ai vu.
Et tu prends un nombre de cas très réduit.

Le 15 avril 2020 à 18:22:46 Doujinologue a écrit :

Le 15 avril 2020 à 18:21:27 RoiLoutre5 a écrit :

Le 15 avril 2020 à 18:15:52 Doujinologue a écrit :
Tout d'abord j'étudie la suite dans la définition [0;+inf[ sans le zéro

On sait qu'un nombre pair est divisé par 2 et qu'un nombre impair multiplié par 3 et +1

Je simplifie la suite de la manière suivante : nous ne travaillerons qu'avec la somme digitale de chaque nombre et résultat

On dresse le tableau suivant en fonction de la parité du nombre départ et de sa somme digitale
Le nombre digital parent est en gras et le nombre digital enfant est souligné

1/2 = 0,5 5
1*3+1 = 4

2/2 = 1
2*3+1 = 7

3/2 = 1,5 6
3*3+1 = 10 1

4/2 = 2
4*3+1 = 13 4

5/2 = 2,5 7
5*3+1 = 16 7

6/2 = 3
6*3+1 = 19 10 1

7/2 = 3,5 8
7*3+1 = 22 4

8/2 = 4
8*3+1 = 25 7

9/2 = 4,5 9
9*3+1 = 28 10 1

On peut dresser l'a figure suivante où grâce à ça
- Les chiffres représentent la somme digitale du nombre X
- Les flèches désignent quelle opération l'ont fait du nombre X (Flèche bleu /2) ( Flèche rouge *3+1)

Ainsi nous voyons que peu importe le nombre de départ on peut atteindre chaque étape et donc tous les nombres sont liés entre eux mais on voit 3 exceptions :

Propiété 1 : Si on ne commence pas par un nombre dont la somme digitale est de 3 6 ou 9 il sera impossible d'en avoir (représenté par les flèches à sens unique)

Proprité 2: On sait aussi que si le nombre X est impair alors le prochain calcul donnera forcément un nombre pair donc flèche rouge

Avec la Propriété2 il ne peut donc pas avoir 2 opérations impairs à la suite

Donc le nombre X aura qu'un nombre égal d'étapes et devra alterner pair et impair pour boucler, car s'il y a que des opérations pairs ou plus d'opérations pair qu'impaire, il tendra vers 1 donc la boucle 4 2 1

Il faut trouver des boucles qui boucles comme : IP , IPIP, IPIPIP etc..

Comme les 9I 6I 3I sont à sens uniques et bouclent sur du pair elles vont tendre vers 1

On doit qu'utiliser les 1I 2I 4I 5I 7I 8I 1P 2P 4P 5P 7P 8P car elle

dans une suite de + de 2 nombres ne doit pas contenir un 7P car il donnera un 8I et bouclera sur 7P8I etc

Etant la seule boucle qui alterne Pair et Impair avec 2 éléments on doit passer à des boucles de 3 éléments ou + et donc exclure 7P et 8I

Boucles possibles : 7P8I

---

Le seul moyen d'accèder à 5 est par un 1P, donc 5P n'est pas disponible

Possibilités restantes : 1I 2I 4I 5I 7I 1P 2P 4P 8P

Donc 5I mènera forcément à 7P, or ce n'est pas une boucle valable donc on supprime 5I
Si on supprime 5I et 5P il faut supprimer 1P qui était le seul chemin qui y menait

Possibilités restantes : 1I 2I 4I 7I 2P 4P 8P

Pour avoir un 8P il faut un 7P or ce n'est pas possible 2P à la suite

Possibilités restantes : 1I 2I 4I 7I 2P 4P

La suite 2I 7I n'est pas possible

Possibilités restantes : 1I 4I 2P 4P

4I ne peut pas boucler sur lui même car seul chemin venant vers 4 et 1I

Possibilités restantes : 1I 2P 4P

Nous avons donc que 2 boucles possibles

1 à 2 éléments : 7P 8I
1 à 3 éléments : 1I 2P 4P

Or selon forumeur vinsmock il est impossible d'alterner infiniment entre pair et impair

Comme une boucle pair impair est impossible le nombre diminuera forcément et donc tendra vers 4P 2P 1I

Based, descopilled et trivial

Tu fais quoi des nombres supérieurs à 9 ? Genre 10 et 11

Leur somme digitale de 10 = 1, 11 = 2, 555555 = 30 3

Mais l'opération de sommation digitale commute pas avec les fonctions n -> 3*n + 1 ou n -> n/2 en fait

Le 15 avril 2020 à 18:25:13 Ghauss3 a écrit :

Le 15 avril 2020 à 18:23:53 Doujinologue a écrit :

Le 15 avril 2020 à 18:22:16 Ghauss3 a écrit :

Le 15 avril 2020 à 18:15:52 Doujinologue a écrit :
Tout d'abord j'étudie la suite dans la définition [0;+inf[ sans le zéro

On sait qu'un nombre pair est divisé par 2 et qu'un nombre impair multiplié par 3 et +1

Je simplifie la suite de la manière suivante : nous ne travaillerons qu'avec la somme digitale de chaque nombre et résultat

On dresse le tableau suivant en fonction de la parité du nombre départ et de sa somme digitale
Le nombre digital parent est en gras et le nombre digital enfant est souligné

1/2 = 0,5 5
1*3+1 = 4

2/2 = 1
2*3+1 = 7

3/2 = 1,5 6
3*3+1 = 10 1

4/2 = 2
4*3+1 = 13 4

5/2 = 2,5 7
5*3+1 = 16 7

6/2 = 3
6*3+1 = 19 10 1

7/2 = 3,5 8
7*3+1 = 22 4

8/2 = 4
8*3+1 = 25 7

9/2 = 4,5 9
9*3+1 = 28 10 1

On peut dresser l'a figure suivante où grâce à ça
- Les chiffres représentent la somme digitale du nombre X
- Les flèches désignent quelle opération l'ont fait du nombre X (Flèche bleu /2) ( Flèche rouge *3+1)

Ainsi nous voyons que peu importe le nombre de départ on peut atteindre chaque étape et donc tous les nombres sont liés entre eux mais on voit 3 exceptions :

Propiété 1 : Si on ne commence pas par un nombre dont la somme digitale est de 3 6 ou 9 il sera impossible d'en avoir (représenté par les flèches à sens unique)

Proprité 2: On sait aussi que si le nombre X est impair alors le prochain calcul donnera forcément un nombre pair donc flèche rouge

Avec la Propriété2 il ne peut donc pas avoir 2 opérations impairs à la suite

Donc le nombre X aura qu'un nombre égal d'étapes et devra alterner pair et impair pour boucler, car s'il y a que des opérations pairs ou plus d'opérations pair qu'impaire, il tendra vers 1 donc la boucle 4 2 1

Il faut trouver des boucles qui boucles comme : IP , IPIP, IPIPIP etc..

Comme les 9I 6I 3I sont à sens uniques et bouclent sur du pair elles vont tendre vers 1

On doit qu'utiliser les 1I 2I 4I 5I 7I 8I 1P 2P 4P 5P 7P 8P car elle

dans une suite de + de 2 nombres ne doit pas contenir un 7P car il donnera un 8I et bouclera sur 7P8I etc

Etant la seule boucle qui alterne Pair et Impair avec 2 éléments on doit passer à des boucles de 3 éléments ou + et donc exclure 7P et 8I

Boucles possibles : 7P8I

---

Le seul moyen d'accèder à 5 est par un 1P, donc 5P n'est pas disponible

Possibilités restantes : 1I 2I 4I 5I 7I 1P 2P 4P 8P

Donc 5I mènera forcément à 7P, or ce n'est pas une boucle valable donc on supprime 5I
Si on supprime 5I et 5P il faut supprimer 1P qui était le seul chemin qui y menait

Possibilités restantes : 1I 2I 4I 7I 2P 4P 8P

Pour avoir un 8P il faut un 7P or ce n'est pas possible 2P à la suite

Possibilités restantes : 1I 2I 4I 7I 2P 4P

La suite 2I 7I n'est pas possible

Possibilités restantes : 1I 4I 2P 4P

4I ne peut pas boucler sur lui même car seul chemin venant vers 4 et 1I

Possibilités restantes : 1I 2P 4P

Nous avons donc que 2 boucles possibles

1 à 2 éléments : 7P 8I
1 à 3 éléments : 1I 2P 4P

Or selon forumeur vinsmock il est impossible d'alterner infiniment entre pair et impair

Comme une boucle pair impair est impossible le nombre diminuera forcément et donc tendra vers 4P 2P 1I

Based, descopilled et trivial

De ce que j'en ai vu, ça m'a l'air faux dès le début avec l'ensemble de travail, puis brouillon avec ton système de notation et ton schéma, ça ne mène pas à grand chose... désolé.
Surtout que là tu n'as absolument pas généralisé.

Comment ça généraliser? Fallait juste démontrer que ça tend vers 4 2 1

Et tu as donc trouvé une séquence qui ne se termine pas par le cycle éternel concrètement ?
Pas vraiment de ce que j'en ai vu.
Et tu prends un nombre de cas très réduit.

Bah non j'ai montré qu'elles tendent toutes vers 4 2 1
C'est de [0;+inf[ comment je peux faire plus grand?

Le 15 avril 2020 à 18:25:39 AdAeternam a écrit :

Le 15 avril 2020 à 18:22:46 Doujinologue a écrit :

Le 15 avril 2020 à 18:21:27 RoiLoutre5 a écrit :

Le 15 avril 2020 à 18:15:52 Doujinologue a écrit :
Tout d'abord j'étudie la suite dans la définition [0;+inf[ sans le zéro

On sait qu'un nombre pair est divisé par 2 et qu'un nombre impair multiplié par 3 et +1

Je simplifie la suite de la manière suivante : nous ne travaillerons qu'avec la somme digitale de chaque nombre et résultat

On dresse le tableau suivant en fonction de la parité du nombre départ et de sa somme digitale
Le nombre digital parent est en gras et le nombre digital enfant est souligné

1/2 = 0,5 5
1*3+1 = 4

2/2 = 1
2*3+1 = 7

3/2 = 1,5 6
3*3+1 = 10 1

4/2 = 2
4*3+1 = 13 4

5/2 = 2,5 7
5*3+1 = 16 7

6/2 = 3
6*3+1 = 19 10 1

7/2 = 3,5 8
7*3+1 = 22 4

8/2 = 4
8*3+1 = 25 7

9/2 = 4,5 9
9*3+1 = 28 10 1

On peut dresser l'a figure suivante où grâce à ça
- Les chiffres représentent la somme digitale du nombre X
- Les flèches désignent quelle opération l'ont fait du nombre X (Flèche bleu /2) ( Flèche rouge *3+1)

Ainsi nous voyons que peu importe le nombre de départ on peut atteindre chaque étape et donc tous les nombres sont liés entre eux mais on voit 3 exceptions :

Propiété 1 : Si on ne commence pas par un nombre dont la somme digitale est de 3 6 ou 9 il sera impossible d'en avoir (représenté par les flèches à sens unique)

Proprité 2: On sait aussi que si le nombre X est impair alors le prochain calcul donnera forcément un nombre pair donc flèche rouge

Avec la Propriété2 il ne peut donc pas avoir 2 opérations impairs à la suite

Donc le nombre X aura qu'un nombre égal d'étapes et devra alterner pair et impair pour boucler, car s'il y a que des opérations pairs ou plus d'opérations pair qu'impaire, il tendra vers 1 donc la boucle 4 2 1

Il faut trouver des boucles qui boucles comme : IP , IPIP, IPIPIP etc..

Comme les 9I 6I 3I sont à sens uniques et bouclent sur du pair elles vont tendre vers 1

On doit qu'utiliser les 1I 2I 4I 5I 7I 8I 1P 2P 4P 5P 7P 8P car elle

dans une suite de + de 2 nombres ne doit pas contenir un 7P car il donnera un 8I et bouclera sur 7P8I etc

Etant la seule boucle qui alterne Pair et Impair avec 2 éléments on doit passer à des boucles de 3 éléments ou + et donc exclure 7P et 8I

Boucles possibles : 7P8I

---

Le seul moyen d'accèder à 5 est par un 1P, donc 5P n'est pas disponible

Possibilités restantes : 1I 2I 4I 5I 7I 1P 2P 4P 8P

Donc 5I mènera forcément à 7P, or ce n'est pas une boucle valable donc on supprime 5I
Si on supprime 5I et 5P il faut supprimer 1P qui était le seul chemin qui y menait

Possibilités restantes : 1I 2I 4I 7I 2P 4P 8P

Pour avoir un 8P il faut un 7P or ce n'est pas possible 2P à la suite

Possibilités restantes : 1I 2I 4I 7I 2P 4P

La suite 2I 7I n'est pas possible

Possibilités restantes : 1I 4I 2P 4P

4I ne peut pas boucler sur lui même car seul chemin venant vers 4 et 1I

Possibilités restantes : 1I 2P 4P

Nous avons donc que 2 boucles possibles

1 à 2 éléments : 7P 8I
1 à 3 éléments : 1I 2P 4P

Or selon forumeur vinsmock il est impossible d'alterner infiniment entre pair et impair

Comme une boucle pair impair est impossible le nombre diminuera forcément et donc tendra vers 4P 2P 1I

Based, descopilled et trivial

Tu fais quoi des nombres supérieurs à 9 ? Genre 10 et 11

Leur somme digitale de 10 = 1, 11 = 2, 555555 = 30 3

Mais l'opération de sommation digitale commute pas avec les fonctions n -> 3*n + 1 ou n -> n/2 en fait

On utilise pas les sommes pour faire l'opération mais pour les liers, tu peux prendre n'importe quel nombre il aura 1 enfant, 1 ou 2 parents ainsi de suite ils sont tous liés, je multiplie pas la somme digitale

Le 15 avril 2020 à 18:28:38 Locustelle a écrit :
Je suis en train de vérifier la preuve de Doujinologue il me reste encore quelques zones d'ombres mais globalement ça semble correct. Dire que personne n'avait jamais pensé à considérer les sommes digitales, c'est tout con mais fallait y penser !

C'est sans doute lié aux propriétés sur les transdiagonales rouges

Le 15 avril 2020 à 18:27:10 Doujinologue a écrit :

Le 15 avril 2020 à 18:25:13 Ghauss3 a écrit :

Le 15 avril 2020 à 18:23:53 Doujinologue a écrit :

Le 15 avril 2020 à 18:22:16 Ghauss3 a écrit :

Le 15 avril 2020 à 18:15:52 Doujinologue a écrit :
Tout d'abord j'étudie la suite dans la définition [0;+inf[ sans le zéro

On sait qu'un nombre pair est divisé par 2 et qu'un nombre impair multiplié par 3 et +1

Je simplifie la suite de la manière suivante : nous ne travaillerons qu'avec la somme digitale de chaque nombre et résultat

On dresse le tableau suivant en fonction de la parité du nombre départ et de sa somme digitale
Le nombre digital parent est en gras et le nombre digital enfant est souligné

1/2 = 0,5 5
1*3+1 = 4

2/2 = 1
2*3+1 = 7

3/2 = 1,5 6
3*3+1 = 10 1

4/2 = 2
4*3+1 = 13 4

5/2 = 2,5 7
5*3+1 = 16 7

6/2 = 3
6*3+1 = 19 10 1

7/2 = 3,5 8
7*3+1 = 22 4

8/2 = 4
8*3+1 = 25 7

9/2 = 4,5 9
9*3+1 = 28 10 1

On peut dresser l'a figure suivante où grâce à ça
- Les chiffres représentent la somme digitale du nombre X
- Les flèches désignent quelle opération l'ont fait du nombre X (Flèche bleu /2) ( Flèche rouge *3+1)

Ainsi nous voyons que peu importe le nombre de départ on peut atteindre chaque étape et donc tous les nombres sont liés entre eux mais on voit 3 exceptions :

Propiété 1 : Si on ne commence pas par un nombre dont la somme digitale est de 3 6 ou 9 il sera impossible d'en avoir (représenté par les flèches à sens unique)

Proprité 2: On sait aussi que si le nombre X est impair alors le prochain calcul donnera forcément un nombre pair donc flèche rouge

Avec la Propriété2 il ne peut donc pas avoir 2 opérations impairs à la suite

Donc le nombre X aura qu'un nombre égal d'étapes et devra alterner pair et impair pour boucler, car s'il y a que des opérations pairs ou plus d'opérations pair qu'impaire, il tendra vers 1 donc la boucle 4 2 1

Il faut trouver des boucles qui boucles comme : IP , IPIP, IPIPIP etc..

Comme les 9I 6I 3I sont à sens uniques et bouclent sur du pair elles vont tendre vers 1

On doit qu'utiliser les 1I 2I 4I 5I 7I 8I 1P 2P 4P 5P 7P 8P car elle

dans une suite de + de 2 nombres ne doit pas contenir un 7P car il donnera un 8I et bouclera sur 7P8I etc

Etant la seule boucle qui alterne Pair et Impair avec 2 éléments on doit passer à des boucles de 3 éléments ou + et donc exclure 7P et 8I

Boucles possibles : 7P8I

---

Le seul moyen d'accèder à 5 est par un 1P, donc 5P n'est pas disponible

Possibilités restantes : 1I 2I 4I 5I 7I 1P 2P 4P 8P

Donc 5I mènera forcément à 7P, or ce n'est pas une boucle valable donc on supprime 5I
Si on supprime 5I et 5P il faut supprimer 1P qui était le seul chemin qui y menait

Possibilités restantes : 1I 2I 4I 7I 2P 4P 8P

Pour avoir un 8P il faut un 7P or ce n'est pas possible 2P à la suite

Possibilités restantes : 1I 2I 4I 7I 2P 4P

La suite 2I 7I n'est pas possible

Possibilités restantes : 1I 4I 2P 4P

4I ne peut pas boucler sur lui même car seul chemin venant vers 4 et 1I

Possibilités restantes : 1I 2P 4P

Nous avons donc que 2 boucles possibles

1 à 2 éléments : 7P 8I
1 à 3 éléments : 1I 2P 4P

Or selon forumeur vinsmock il est impossible d'alterner infiniment entre pair et impair

Comme une boucle pair impair est impossible le nombre diminuera forcément et donc tendra vers 4P 2P 1I

Based, descopilled et trivial

De ce que j'en ai vu, ça m'a l'air faux dès le début avec l'ensemble de travail, puis brouillon avec ton système de notation et ton schéma, ça ne mène pas à grand chose... désolé.
Surtout que là tu n'as absolument pas généralisé.

Comment ça généraliser? Fallait juste démontrer que ça tend vers 4 2 1

Et tu as donc trouvé une séquence qui ne se termine pas par le cycle éternel concrètement ?
Pas vraiment de ce que j'en ai vu.
Et tu prends un nombre de cas très réduit.

Bah non j'ai montré qu'elles tendent toutes vers 4 2 1
C'est de [0;+inf[ comment je peux faire plus grand?

Je suis entrain de relire pour voir atteint, donc ton idée globale c'est de montrer que pour tout n, la suite convergera forcément vers 4 2 1 en utilisant leurs sommes digitales ?

Le 15 avril 2020 à 18:30:10 Ghauss3 a écrit :

Le 15 avril 2020 à 18:27:10 Doujinologue a écrit :

Le 15 avril 2020 à 18:25:13 Ghauss3 a écrit :

Le 15 avril 2020 à 18:23:53 Doujinologue a écrit :

Le 15 avril 2020 à 18:22:16 Ghauss3 a écrit :

Le 15 avril 2020 à 18:15:52 Doujinologue a écrit :
Tout d'abord j'étudie la suite dans la définition [0;+inf[ sans le zéro

On sait qu'un nombre pair est divisé par 2 et qu'un nombre impair multiplié par 3 et +1

Je simplifie la suite de la manière suivante : nous ne travaillerons qu'avec la somme digitale de chaque nombre et résultat

On dresse le tableau suivant en fonction de la parité du nombre départ et de sa somme digitale
Le nombre digital parent est en gras et le nombre digital enfant est souligné

1/2 = 0,5 5
1*3+1 = 4

2/2 = 1
2*3+1 = 7

3/2 = 1,5 6
3*3+1 = 10 1

4/2 = 2
4*3+1 = 13 4

5/2 = 2,5 7
5*3+1 = 16 7

6/2 = 3
6*3+1 = 19 10 1

7/2 = 3,5 8
7*3+1 = 22 4

8/2 = 4
8*3+1 = 25 7

9/2 = 4,5 9
9*3+1 = 28 10 1

On peut dresser l'a figure suivante où grâce à ça
- Les chiffres représentent la somme digitale du nombre X
- Les flèches désignent quelle opération l'ont fait du nombre X (Flèche bleu /2) ( Flèche rouge *3+1)

Ainsi nous voyons que peu importe le nombre de départ on peut atteindre chaque étape et donc tous les nombres sont liés entre eux mais on voit 3 exceptions :

Propiété 1 : Si on ne commence pas par un nombre dont la somme digitale est de 3 6 ou 9 il sera impossible d'en avoir (représenté par les flèches à sens unique)

Proprité 2: On sait aussi que si le nombre X est impair alors le prochain calcul donnera forcément un nombre pair donc flèche rouge

Avec la Propriété2 il ne peut donc pas avoir 2 opérations impairs à la suite

Donc le nombre X aura qu'un nombre égal d'étapes et devra alterner pair et impair pour boucler, car s'il y a que des opérations pairs ou plus d'opérations pair qu'impaire, il tendra vers 1 donc la boucle 4 2 1

Il faut trouver des boucles qui boucles comme : IP , IPIP, IPIPIP etc..

Comme les 9I 6I 3I sont à sens uniques et bouclent sur du pair elles vont tendre vers 1

On doit qu'utiliser les 1I 2I 4I 5I 7I 8I 1P 2P 4P 5P 7P 8P car elle

dans une suite de + de 2 nombres ne doit pas contenir un 7P car il donnera un 8I et bouclera sur 7P8I etc

Etant la seule boucle qui alterne Pair et Impair avec 2 éléments on doit passer à des boucles de 3 éléments ou + et donc exclure 7P et 8I

Boucles possibles : 7P8I

---

Le seul moyen d'accèder à 5 est par un 1P, donc 5P n'est pas disponible

Possibilités restantes : 1I 2I 4I 5I 7I 1P 2P 4P 8P

Donc 5I mènera forcément à 7P, or ce n'est pas une boucle valable donc on supprime 5I
Si on supprime 5I et 5P il faut supprimer 1P qui était le seul chemin qui y menait

Possibilités restantes : 1I 2I 4I 7I 2P 4P 8P

Pour avoir un 8P il faut un 7P or ce n'est pas possible 2P à la suite

Possibilités restantes : 1I 2I 4I 7I 2P 4P

La suite 2I 7I n'est pas possible

Possibilités restantes : 1I 4I 2P 4P

4I ne peut pas boucler sur lui même car seul chemin venant vers 4 et 1I

Possibilités restantes : 1I 2P 4P

Nous avons donc que 2 boucles possibles

1 à 2 éléments : 7P 8I
1 à 3 éléments : 1I 2P 4P

Or selon forumeur vinsmock il est impossible d'alterner infiniment entre pair et impair

Comme une boucle pair impair est impossible le nombre diminuera forcément et donc tendra vers 4P 2P 1I

Based, descopilled et trivial

De ce que j'en ai vu, ça m'a l'air faux dès le début avec l'ensemble de travail, puis brouillon avec ton système de notation et ton schéma, ça ne mène pas à grand chose... désolé.
Surtout que là tu n'as absolument pas généralisé.

Comment ça généraliser? Fallait juste démontrer que ça tend vers 4 2 1

Et tu as donc trouvé une séquence qui ne se termine pas par le cycle éternel concrètement ?
Pas vraiment de ce que j'en ai vu.
Et tu prends un nombre de cas très réduit.

Bah non j'ai montré qu'elles tendent toutes vers 4 2 1
C'est de [0;+inf[ comment je peux faire plus grand?

Je suis entrain de relire pour voir atteint, donc ton idée globale c'est de montrer que pour tout n, la suite convergera forcément vers 4 2 1 en utilisant leurs sommes digitales ?

C'est ça

Le 15 avril 2020 à 18:30:52 Dropthezitounes a écrit :
Bon alors vous avez l'avoir votre médaille ou pas ? Ça traîne la pour l'élite..

On analyse une proposition sérieuse là

On est en pleine session du comité de relecture

Le 15 avril 2020 à 18:28:42 Doujinologue a écrit :

Le 15 avril 2020 à 18:25:39 AdAeternam a écrit :

Le 15 avril 2020 à 18:22:46 Doujinologue a écrit :

Le 15 avril 2020 à 18:21:27 RoiLoutre5 a écrit :

Le 15 avril 2020 à 18:15:52 Doujinologue a écrit :
Tout d'abord j'étudie la suite dans la définition [0;+inf[ sans le zéro

On sait qu'un nombre pair est divisé par 2 et qu'un nombre impair multiplié par 3 et +1

Je simplifie la suite de la manière suivante : nous ne travaillerons qu'avec la somme digitale de chaque nombre et résultat

On dresse le tableau suivant en fonction de la parité du nombre départ et de sa somme digitale
Le nombre digital parent est en gras et le nombre digital enfant est souligné

1/2 = 0,5 5
1*3+1 = 4

2/2 = 1
2*3+1 = 7

3/2 = 1,5 6
3*3+1 = 10 1

4/2 = 2
4*3+1 = 13 4

5/2 = 2,5 7
5*3+1 = 16 7

6/2 = 3
6*3+1 = 19 10 1

7/2 = 3,5 8
7*3+1 = 22 4

8/2 = 4
8*3+1 = 25 7

9/2 = 4,5 9
9*3+1 = 28 10 1

On peut dresser l'a figure suivante où grâce à ça
- Les chiffres représentent la somme digitale du nombre X
- Les flèches désignent quelle opération l'ont fait du nombre X (Flèche bleu /2) ( Flèche rouge *3+1)

Ainsi nous voyons que peu importe le nombre de départ on peut atteindre chaque étape et donc tous les nombres sont liés entre eux mais on voit 3 exceptions :

Propiété 1 : Si on ne commence pas par un nombre dont la somme digitale est de 3 6 ou 9 il sera impossible d'en avoir (représenté par les flèches à sens unique)

Proprité 2: On sait aussi que si le nombre X est impair alors le prochain calcul donnera forcément un nombre pair donc flèche rouge

Avec la Propriété2 il ne peut donc pas avoir 2 opérations impairs à la suite

Donc le nombre X aura qu'un nombre égal d'étapes et devra alterner pair et impair pour boucler, car s'il y a que des opérations pairs ou plus d'opérations pair qu'impaire, il tendra vers 1 donc la boucle 4 2 1

Il faut trouver des boucles qui boucles comme : IP , IPIP, IPIPIP etc..

Comme les 9I 6I 3I sont à sens uniques et bouclent sur du pair elles vont tendre vers 1

On doit qu'utiliser les 1I 2I 4I 5I 7I 8I 1P 2P 4P 5P 7P 8P car elle

dans une suite de + de 2 nombres ne doit pas contenir un 7P car il donnera un 8I et bouclera sur 7P8I etc

Etant la seule boucle qui alterne Pair et Impair avec 2 éléments on doit passer à des boucles de 3 éléments ou + et donc exclure 7P et 8I

Boucles possibles : 7P8I

---

Le seul moyen d'accèder à 5 est par un 1P, donc 5P n'est pas disponible

Possibilités restantes : 1I 2I 4I 5I 7I 1P 2P 4P 8P

Donc 5I mènera forcément à 7P, or ce n'est pas une boucle valable donc on supprime 5I
Si on supprime 5I et 5P il faut supprimer 1P qui était le seul chemin qui y menait

Possibilités restantes : 1I 2I 4I 7I 2P 4P 8P

Pour avoir un 8P il faut un 7P or ce n'est pas possible 2P à la suite

Possibilités restantes : 1I 2I 4I 7I 2P 4P

La suite 2I 7I n'est pas possible

Possibilités restantes : 1I 4I 2P 4P

4I ne peut pas boucler sur lui même car seul chemin venant vers 4 et 1I

Possibilités restantes : 1I 2P 4P

Nous avons donc que 2 boucles possibles

1 à 2 éléments : 7P 8I
1 à 3 éléments : 1I 2P 4P

Or selon forumeur vinsmock il est impossible d'alterner infiniment entre pair et impair

Comme une boucle pair impair est impossible le nombre diminuera forcément et donc tendra vers 4P 2P 1I

Based, descopilled et trivial

Tu fais quoi des nombres supérieurs à 9 ? Genre 10 et 11

Leur somme digitale de 10 = 1, 11 = 2, 555555 = 30 3

Mais l'opération de sommation digitale commute pas avec les fonctions n -> 3*n + 1 ou n -> n/2 en fait

On utilise pas les sommes pour faire l'opération mais pour les liers, tu peux prendre n'importe quel nombre il aura 1 enfant, 1 ou 2 parents ainsi de suite ils sont tous liés, je multiplie pas la somme digitale

Non mais même, puisque ça commute pas ce que tu racontes n'a aucun sens.
Tu peux pas appliquer la transformation affine après la somme digitale et faire comme si c'était la somme digitale de la transformée affine

car s'il y a que des opérations pairs ou plus d'opérations pair qu'impaire, il tendra vers 1 donc la boucle 4 2 1

à prouver

On va oublier le "+1" dans l'opération "3n+1" pour le moment.
Je prends un nombre, je fais des milliards de fois les opérations "multiplier par 3" ou " diviser par 2" avec ce nombre, je pourrais très bien diviser par deux plus fréquemment que je ne multiplie par 3 et pour autant augmenter énormément la valeur de mon nombre, tout simplement car une multiplication par 3 c'est plus "puissant" qu'une division par 2.

Pour le reste je ne commente pas pour l'instant, j'ai du mal à comprendre ce que tu racontes tout en regardant le live Myriogon

Le 15 avril 2020 à 18:32:35 Doujinologue a écrit :
Le seul moyen de me montrer que j'ai tort que j'ia trouvé, c'est de trouver un nombre avec une somme digitale qui n'est pas comprise entre 1 et 9

555

Putain mais ça devrait être interdit les topics de maths aux descos qui ont clairement même pas de bac S

Vous vous rendez compte que tout ce que vous écrivez n'a aucun sens ?

Le pire c'est qu'ils font semblent de se comprendre entre eux parce qu'ils croient que ça leur donne de la math-cred

Le 15 avril 2020 à 18:32:43 AdAeternam a écrit :

Le 15 avril 2020 à 18:28:42 Doujinologue a écrit :

Le 15 avril 2020 à 18:25:39 AdAeternam a écrit :

Le 15 avril 2020 à 18:22:46 Doujinologue a écrit :

Le 15 avril 2020 à 18:21:27 RoiLoutre5 a écrit :

Le 15 avril 2020 à 18:15:52 Doujinologue a écrit :
Tout d'abord j'étudie la suite dans la définition [0;+inf[ sans le zéro

On sait qu'un nombre pair est divisé par 2 et qu'un nombre impair multiplié par 3 et +1

Je simplifie la suite de la manière suivante : nous ne travaillerons qu'avec la somme digitale de chaque nombre et résultat

On dresse le tableau suivant en fonction de la parité du nombre départ et de sa somme digitale
Le nombre digital parent est en gras et le nombre digital enfant est souligné

1/2 = 0,5 5
1*3+1 = 4

2/2 = 1
2*3+1 = 7

3/2 = 1,5 6
3*3+1 = 10 1

4/2 = 2
4*3+1 = 13 4

5/2 = 2,5 7
5*3+1 = 16 7

6/2 = 3
6*3+1 = 19 10 1

7/2 = 3,5 8
7*3+1 = 22 4

8/2 = 4
8*3+1 = 25 7

9/2 = 4,5 9
9*3+1 = 28 10 1

On peut dresser l'a figure suivante où grâce à ça
- Les chiffres représentent la somme digitale du nombre X
- Les flèches désignent quelle opération l'ont fait du nombre X (Flèche bleu /2) ( Flèche rouge *3+1)

Ainsi nous voyons que peu importe le nombre de départ on peut atteindre chaque étape et donc tous les nombres sont liés entre eux mais on voit 3 exceptions :

Propiété 1 : Si on ne commence pas par un nombre dont la somme digitale est de 3 6 ou 9 il sera impossible d'en avoir (représenté par les flèches à sens unique)

Proprité 2: On sait aussi que si le nombre X est impair alors le prochain calcul donnera forcément un nombre pair donc flèche rouge

Avec la Propriété2 il ne peut donc pas avoir 2 opérations impairs à la suite

Donc le nombre X aura qu'un nombre égal d'étapes et devra alterner pair et impair pour boucler, car s'il y a que des opérations pairs ou plus d'opérations pair qu'impaire, il tendra vers 1 donc la boucle 4 2 1

Il faut trouver des boucles qui boucles comme : IP , IPIP, IPIPIP etc..

Comme les 9I 6I 3I sont à sens uniques et bouclent sur du pair elles vont tendre vers 1

On doit qu'utiliser les 1I 2I 4I 5I 7I 8I 1P 2P 4P 5P 7P 8P car elle

dans une suite de + de 2 nombres ne doit pas contenir un 7P car il donnera un 8I et bouclera sur 7P8I etc

Etant la seule boucle qui alterne Pair et Impair avec 2 éléments on doit passer à des boucles de 3 éléments ou + et donc exclure 7P et 8I

Boucles possibles : 7P8I

---

Le seul moyen d'accèder à 5 est par un 1P, donc 5P n'est pas disponible

Possibilités restantes : 1I 2I 4I 5I 7I 1P 2P 4P 8P

Donc 5I mènera forcément à 7P, or ce n'est pas une boucle valable donc on supprime 5I
Si on supprime 5I et 5P il faut supprimer 1P qui était le seul chemin qui y menait

Possibilités restantes : 1I 2I 4I 7I 2P 4P 8P

Pour avoir un 8P il faut un 7P or ce n'est pas possible 2P à la suite

Possibilités restantes : 1I 2I 4I 7I 2P 4P

La suite 2I 7I n'est pas possible

Possibilités restantes : 1I 4I 2P 4P

4I ne peut pas boucler sur lui même car seul chemin venant vers 4 et 1I

Possibilités restantes : 1I 2P 4P

Nous avons donc que 2 boucles possibles

1 à 2 éléments : 7P 8I
1 à 3 éléments : 1I 2P 4P

Or selon forumeur vinsmock il est impossible d'alterner infiniment entre pair et impair

Comme une boucle pair impair est impossible le nombre diminuera forcément et donc tendra vers 4P 2P 1I

Based, descopilled et trivial

Tu fais quoi des nombres supérieurs à 9 ? Genre 10 et 11

Leur somme digitale de 10 = 1, 11 = 2, 555555 = 30 3

Mais l'opération de sommation digitale commute pas avec les fonctions n -> 3*n + 1 ou n -> n/2 en fait

On utilise pas les sommes pour faire l'opération mais pour les liers, tu peux prendre n'importe quel nombre il aura 1 enfant, 1 ou 2 parents ainsi de suite ils sont tous liés, je multiplie pas la somme digitale

Non mais même, puisque ça commute pas ce que tu racontes n'a aucun sens.
Tu peux pas appliquer la transformation affine après la somme digitale et faire comme si c'était la somme digitale de la transformée affine

Pas compris ce que tu veux dire

Le 15 avril 2020 à 18:33:23 RoiLoutre5 a écrit :

Le 15 avril 2020 à 18:32:35 Doujinologue a écrit :
Le seul moyen de me montrer que j'ai tort que j'ia trouvé, c'est de trouver un nombre avec une somme digitale qui n'est pas comprise entre 1 et 9

555

Ça fait 1+0+5 = 6