[MATHS] Pensez-vous qu'à nous tous nous puissions résoudre la conjecture de Syracuse ?
Le 15 avril 2020 à 18:10:27 Drayon a écrit :
Rassurez moi ce topic c'est quand même pas 60 pages de descos qui essaient sérieusement de démontrer la conjecture de Syracuse svp ?
Horizontale blue en effet. 
Non sérieusement personne n'essaye sérieusement de la démontrer, les gens regardent, test et discutent, ou essayent de discuter sur le sujet. Et puis je ne vois pas de descos. 

Le 15 avril 2020 à 18:13:43 Dwire2 a écrit :
Bah c'est simple il suffit de vérifier que la conjecture est vraie pour tous les entiers, quand on les aura tous testé on aura la réponse
.gif)
Le 15 avril 2020 à 18:13:43 Dwire2 a écrit :
Bah c'est simple il suffit de vérifier que la conjecture est vraie pour tous les entiers, quand on les aura tous testé on aura la réponse
Elle est fausse pour 0 et plus généralement pour les négatifs 
Le 15 avril 2020 à 18:14:16 Vinsmock a écrit :
Le 15 avril 2020 à 18:13:43 Dwire2 a écrit :
Bah c'est simple il suffit de vérifier que la conjecture est vraie pour tous les entiers, quand on les aura tous testé on aura la réponseElle est fausse pour 0 et plus généralement pour les négatifs
Tout d'abord j'étudie la suite dans la définition [0;+inf[ sans le zéro
On sait qu'un nombre pair est divisé par 2 et qu'un nombre impair multiplié par 3 et +1
Je simplifie la suite de la manière suivante : nous ne travaillerons qu'avec la somme digitale de chaque nombre et résultat
On dresse le tableau suivant en fonction de la parité du nombre départ et de sa somme digitale
Le nombre digital parent est en gras et le nombre digital enfant est souligné
1/2 = 0,5 .gif) 5
5
1*3+1 = 4
2/2 = 1
2*3+1 = 7
3/2 = 1,5 .gif) 6
6
3*3+1 = 10 .gif) 1
1
4/2 = 2
4*3+1 = 13 .gif) 4
4
5/2 = 2,5 .gif) 7
7
5*3+1 = 16 .gif) 7
7
6/2 = 3
6*3+1 = 19 .gif) 10
10 .gif) 1
1
7/2 = 3,5 .gif) 8
8
7*3+1 = 22 .gif) 4
4
8/2 = 4
8*3+1 = 25 .gif) 7
7
9/2 = 4,5 .gif) 9
9
9*3+1 = 28 .gif) 10
10 .gif) 1
1
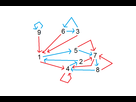
On peut dresser l'a figure suivante où grâce à ça
- Les chiffres représentent la somme digitale du nombre X
- Les flèches désignent quelle opération l'ont fait du nombre X (Flèche bleu .gif) /2) ( Flèche rouge
/2) ( Flèche rouge .gif) *3+1)
*3+1)
Ainsi nous voyons que peu importe le nombre de départ on peut atteindre chaque étape et donc tous les nombres sont liés entre eux mais on voit 3 exceptions :
Propiété 1 : Si on ne commence pas par un nombre dont la somme digitale est de 3 6 ou 9 il sera impossible d'en avoir (représenté par les flèches à sens unique)
Proprité 2: On sait aussi que si le nombre X est impair alors le prochain calcul donnera forcément un nombre pair donc flèche rouge
Avec la Propriété2 il ne peut donc pas avoir 2 opérations impairs à la suite
Donc le nombre X aura qu'un nombre égal d'étapes et devra alterner pair et impair pour boucler, car s'il y a que des opérations pairs ou plus d'opérations pair qu'impaire, il tendra vers 1 donc la boucle 4 2 1
Il faut trouver des boucles qui boucles comme : IP , IPIP, IPIPIP etc..
Comme les 9I 6I 3I sont à sens uniques et bouclent sur du pair elles vont tendre vers 1
On doit qu'utiliser les 1I 2I 4I 5I 7I 8I 1P 2P 4P 5P 7P 8P car elle
dans une suite de + de 2 nombres ne doit pas contenir un 7P car il donnera un 8I et bouclera sur 7P8I etc
Etant la seule boucle qui alterne Pair et Impair avec 2 éléments on doit passer à des boucles de 3 éléments ou + et donc exclure 7P et 8I
Boucles possibles : 7P8I
---
Le seul moyen d'accèder à 5 est par un 1P, donc 5P n'est pas disponible
Possibilités restantes : 1I 2I 4I 5I 7I 1P 2P 4P 8P
Donc 5I mènera forcément à 7P, or ce n'est pas une boucle valable donc on supprime 5I
Si on supprime 5I et 5P il faut supprimer 1P qui était le seul chemin qui y menait
Possibilités restantes : 1I 2I 4I 7I 2P 4P 8P
Pour avoir un 8P il faut un 7P or ce n'est pas possible 2P à la suite
Possibilités restantes : 1I 2I 4I 7I 2P 4P
La suite 2I 7I n'est pas possible
Possibilités restantes : 1I 4I 2P 4P
4I ne peut pas boucler sur lui même car seul chemin venant vers 4 et 1I
Possibilités restantes : 1I 2P 4P
Nous avons donc que 2 boucles possibles
1 à 2 éléments : 7P 8I
1 à 3 éléments : 1I 2P 4P
Or selon forumeur vinsmock il est impossible d'alterner infiniment entre pair et impair
Comme une boucle pair impair est impossible le nombre diminuera forcément et donc tendra vers 4P 2P 1I

Le 15 avril 2020 à 18:15:52 Doujinologue a écrit :
Tout d'abord j'étudie la suite dans la définition [0;+inf[ sans le zéroOn sait qu'un nombre pair est divisé par 2 et qu'un nombre impair multiplié par 3 et +1
Je simplifie la suite de la manière suivante : nous ne travaillerons qu'avec la somme digitale de chaque nombre et résultat
On dresse le tableau suivant en fonction de la parité du nombre départ et de sa somme digitale
Le nombre digital parent est en gras et le nombre digital enfant est souligné1/2 = 0,5
5
1*3+1 = 42/2 = 1
2*3+1 = 73/2 = 1,5
6
3*3+1 = 101
4/2 = 2
4*3+1 = 134
5/2 = 2,5
7
5*3+1 = 167
6/2 = 3
6*3+1 = 1910
1
7/2 = 3,5
8
7*3+1 = 224
8/2 = 4
8*3+1 = 257
9/2 = 4,5
9
9*3+1 = 2810
1
On peut dresser l'a figure suivante où grâce à ça
- Les chiffres représentent la somme digitale du nombre X
- Les flèches désignent quelle opération l'ont fait du nombre X (Flèche bleu/2) ( Flèche rouge
*3+1)
Ainsi nous voyons que peu importe le nombre de départ on peut atteindre chaque étape et donc tous les nombres sont liés entre eux mais on voit 3 exceptions :
Propiété 1 : Si on ne commence pas par un nombre dont la somme digitale est de 3 6 ou 9 il sera impossible d'en avoir (représenté par les flèches à sens unique)
Proprité 2: On sait aussi que si le nombre X est impair alors le prochain calcul donnera forcément un nombre pair donc flèche rouge
Avec la Propriété2 il ne peut donc pas avoir 2 opérations impairs à la suite
Donc le nombre X aura qu'un nombre égal d'étapes et devra alterner pair et impair pour boucler, car s'il y a que des opérations pairs ou plus d'opérations pair qu'impaire, il tendra vers 1 donc la boucle 4 2 1
Il faut trouver des boucles qui boucles comme : IP , IPIP, IPIPIP etc..
Comme les 9I 6I 3I sont à sens uniques et bouclent sur du pair elles vont tendre vers 1
On doit qu'utiliser les 1I 2I 4I 5I 7I 8I 1P 2P 4P 5P 7P 8P car elle
dans une suite de + de 2 nombres ne doit pas contenir un 7P car il donnera un 8I et bouclera sur 7P8I etc
Etant la seule boucle qui alterne Pair et Impair avec 2 éléments on doit passer à des boucles de 3 éléments ou + et donc exclure 7P et 8I
Boucles possibles : 7P8I
---
Le seul moyen d'accèder à 5 est par un 1P, donc 5P n'est pas disponible
Possibilités restantes : 1I 2I 4I 5I 7I 1P 2P 4P 8P
Donc 5I mènera forcément à 7P, or ce n'est pas une boucle valable donc on supprime 5I
Si on supprime 5I et 5P il faut supprimer 1P qui était le seul chemin qui y menaitPossibilités restantes : 1I 2I 4I 7I 2P 4P 8P
Pour avoir un 8P il faut un 7P or ce n'est pas possible 2P à la suite
Possibilités restantes : 1I 2I 4I 7I 2P 4P
La suite 2I 7I n'est pas possible
Possibilités restantes : 1I 4I 2P 4P
4I ne peut pas boucler sur lui même car seul chemin venant vers 4 et 1I
Possibilités restantes : 1I 2P 4P
Nous avons donc que 2 boucles possibles
1 à 2 éléments : 7P 8I
1 à 3 éléments : 1I 2P 4POr selon forumeur vinsmock il est impossible d'alterner infiniment entre pair et impair
Comme une boucle pair impair est impossible le nombre diminuera forcément et donc tendra vers 4P 2P 1I
Merci, a moi la médail fields .gif)
Le 15 avril 2020 à 18:16:07 Drayon a écrit :
Ah oui oui je vois ça doit être très "enrichissant" de discuter de ses idées de preuve de Syracuse pendant 60 pages sur le 18-25, c'est certainement pas une lubie de descos
C'est le confinement monsieur, il n'y a pas beaucoup de descos ici non, que des matheux, ou peut-être 1 ou 2 matheux descos, les vrais descos sont sur les topics de déchets. 
Et c'est bon non plus hein, on parle de mathématiques où on veut quand on veut, mais le mieux est d'en parler partout. 
Bon j'essaye de rattraper tout le topic pour me mettre à niveau sur le problème mais c'est long.
En attendant voici les quelques resultat que j'avait obtenue lors d'une heure de CDI en première:
-Premièrement changer le 3 du 3n+1: notons a la constante multiplicative
-Si a paire alors a(2m+1)+1= 2am+a+1 qui est impaire, la suite s'envol vers l'infini au premier impaire
-Si a impaire : a=1 : ((2m+1)+1)/2 strictement inferieur à 2m+1 donc la suite converge vers le cycle
1;2;1;2
a=5 : on a le cycle 1;6;3;16;8;4;2;1 ainsi que le cycle 13;66;33;166;83;416;208;104;52;26;13. J'en ai pas chercher d'autre mais tout les entier différents de zéro neconvergent pas vers le même cycle
Sinon pour le cas a=3 qui nous intéresse j'avais tenté une récurence forte:
initialisation: vrai jusqu'a 10^100 (c'est important)
hérédité: supposons syracuse vérifié jusqu'à n>10^100 alors on peut faire l'approximation (3n+1)/2 = 3n/2
n à 50% de chance d'etre paire auquel cas la prochaine étape sera n/2<n qui est vérifié dans l'autre cas la prochaine étape vaudra 3n/2 qui à lui meme 50% de chance d'etre paire et qui vaudra donc à la prochaine étape 3n/4 < n et donc vérifié.
on a ainsi éliminé 75% des cas. en continuant le raisonnement on montre que la probabilté que n ne soit pas vérifié tant vers 0. et donc syracuse est vérifié
Le 15 avril 2020 à 17:58:08 Doujinologue a écrit :
Si j'arrive à prouver que la boucle pair impair ne peut pas se continuer infiniment j'ai démontré la conjecture
Putain mais c'est possible que tu puisses parler de manière pédagogue ? 
J'ai lu les 58 pages et franchement j'ai vraiment l'impression de lire un truc que Perceval de Kaamelott écrirait. Ton schéma est une représentation artistique d'un AVC, et ton ton pédant "ouais c'est bon j'ai démontré" est insupportable. 
Franchement essaie de décrire les termes que tu utilises et explique toi plus en détails. A chaque fois que t'as écrit un post on t'a repris pour de demander de clarifier. 
C'est le stéreotype vivant du mec qui prétend de trouver un modèle de la gravitation quantique. 
Le 15 avril 2020 à 18:20:02 VelvetThunder a écrit :
Le 15 avril 2020 à 17:58:08 Doujinologue a écrit :
Si j'arrive à prouver que la boucle pair impair ne peut pas se continuer infiniment j'ai démontré la conjecturePutain mais c'est possible que tu puisses parler de manière pédagogue ?

J'ai lu les 58 pages et franchement j'ai vraiment l'impression de lire un truc que Perceval de Kaamelott écrirait. Ton schéma est une représentation artistique d'un AVC, et ton ton pédant "ouais c'est bon j'ai démontré" est insupportable.
Franchement essaie de décrire les termes que tu utilises et explique toi plus en détails. A chaque fois que t'as écrit un post on t'a repris pour de demander de clarifier.

C'est le stéreotype vivant du mec qui prétend de trouver un modèle de la gravitation quantique.

Au moins je tente et toi? 
La gravitation quantique je te la fais en 5 minutes easy 
Le 15 avril 2020 à 18:15:52 Doujinologue a écrit :
Tout d'abord j'étudie la suite dans la définition [0;+inf[ sans le zéroOn sait qu'un nombre pair est divisé par 2 et qu'un nombre impair multiplié par 3 et +1
Je simplifie la suite de la manière suivante : nous ne travaillerons qu'avec la somme digitale de chaque nombre et résultat
On dresse le tableau suivant en fonction de la parité du nombre départ et de sa somme digitale
Le nombre digital parent est en gras et le nombre digital enfant est souligné1/2 = 0,5
5
1*3+1 = 42/2 = 1
2*3+1 = 73/2 = 1,5
6
3*3+1 = 101
4/2 = 2
4*3+1 = 134
5/2 = 2,5
7
5*3+1 = 167
6/2 = 3
6*3+1 = 1910
1
7/2 = 3,5
8
7*3+1 = 224
8/2 = 4
8*3+1 = 257
9/2 = 4,5
9
9*3+1 = 2810
1
On peut dresser l'a figure suivante où grâce à ça
- Les chiffres représentent la somme digitale du nombre X
- Les flèches désignent quelle opération l'ont fait du nombre X (Flèche bleu/2) ( Flèche rouge
*3+1)
Ainsi nous voyons que peu importe le nombre de départ on peut atteindre chaque étape et donc tous les nombres sont liés entre eux mais on voit 3 exceptions :
Propiété 1 : Si on ne commence pas par un nombre dont la somme digitale est de 3 6 ou 9 il sera impossible d'en avoir (représenté par les flèches à sens unique)
Proprité 2: On sait aussi que si le nombre X est impair alors le prochain calcul donnera forcément un nombre pair donc flèche rouge
Avec la Propriété2 il ne peut donc pas avoir 2 opérations impairs à la suite
Donc le nombre X aura qu'un nombre égal d'étapes et devra alterner pair et impair pour boucler, car s'il y a que des opérations pairs ou plus d'opérations pair qu'impaire, il tendra vers 1 donc la boucle 4 2 1
Il faut trouver des boucles qui boucles comme : IP , IPIP, IPIPIP etc..
Comme les 9I 6I 3I sont à sens uniques et bouclent sur du pair elles vont tendre vers 1
On doit qu'utiliser les 1I 2I 4I 5I 7I 8I 1P 2P 4P 5P 7P 8P car elle
dans une suite de + de 2 nombres ne doit pas contenir un 7P car il donnera un 8I et bouclera sur 7P8I etc
Etant la seule boucle qui alterne Pair et Impair avec 2 éléments on doit passer à des boucles de 3 éléments ou + et donc exclure 7P et 8I
Boucles possibles : 7P8I
---
Le seul moyen d'accèder à 5 est par un 1P, donc 5P n'est pas disponible
Possibilités restantes : 1I 2I 4I 5I 7I 1P 2P 4P 8P
Donc 5I mènera forcément à 7P, or ce n'est pas une boucle valable donc on supprime 5I
Si on supprime 5I et 5P il faut supprimer 1P qui était le seul chemin qui y menaitPossibilités restantes : 1I 2I 4I 7I 2P 4P 8P
Pour avoir un 8P il faut un 7P or ce n'est pas possible 2P à la suite
Possibilités restantes : 1I 2I 4I 7I 2P 4P
La suite 2I 7I n'est pas possible
Possibilités restantes : 1I 4I 2P 4P
4I ne peut pas boucler sur lui même car seul chemin venant vers 4 et 1I
Possibilités restantes : 1I 2P 4P
Nous avons donc que 2 boucles possibles
1 à 2 éléments : 7P 8I
1 à 3 éléments : 1I 2P 4POr selon forumeur vinsmock il est impossible d'alterner infiniment entre pair et impair
Comme une boucle pair impair est impossible le nombre diminuera forcément et donc tendra vers 4P 2P 1I
Le 15 avril 2020 à 18:15:52 Doujinologue a écrit :
Tout d'abord j'étudie la suite dans la définition [0;+inf[ sans le zéroOn sait qu'un nombre pair est divisé par 2 et qu'un nombre impair multiplié par 3 et +1
Je simplifie la suite de la manière suivante : nous ne travaillerons qu'avec la somme digitale de chaque nombre et résultat
On dresse le tableau suivant en fonction de la parité du nombre départ et de sa somme digitale
Le nombre digital parent est en gras et le nombre digital enfant est souligné1/2 = 0,5
5
1*3+1 = 42/2 = 1
2*3+1 = 73/2 = 1,5
6
3*3+1 = 101
4/2 = 2
4*3+1 = 134
5/2 = 2,5
7
5*3+1 = 167
6/2 = 3
6*3+1 = 1910
1
7/2 = 3,5
8
7*3+1 = 224
8/2 = 4
8*3+1 = 257
9/2 = 4,5
9
9*3+1 = 2810
1
On peut dresser l'a figure suivante où grâce à ça
- Les chiffres représentent la somme digitale du nombre X
- Les flèches désignent quelle opération l'ont fait du nombre X (Flèche bleu/2) ( Flèche rouge
*3+1)
Ainsi nous voyons que peu importe le nombre de départ on peut atteindre chaque étape et donc tous les nombres sont liés entre eux mais on voit 3 exceptions :
Propiété 1 : Si on ne commence pas par un nombre dont la somme digitale est de 3 6 ou 9 il sera impossible d'en avoir (représenté par les flèches à sens unique)
Proprité 2: On sait aussi que si le nombre X est impair alors le prochain calcul donnera forcément un nombre pair donc flèche rouge
Avec la Propriété2 il ne peut donc pas avoir 2 opérations impairs à la suite
Donc le nombre X aura qu'un nombre égal d'étapes et devra alterner pair et impair pour boucler, car s'il y a que des opérations pairs ou plus d'opérations pair qu'impaire, il tendra vers 1 donc la boucle 4 2 1
Il faut trouver des boucles qui boucles comme : IP , IPIP, IPIPIP etc..
Comme les 9I 6I 3I sont à sens uniques et bouclent sur du pair elles vont tendre vers 1
On doit qu'utiliser les 1I 2I 4I 5I 7I 8I 1P 2P 4P 5P 7P 8P car elle
dans une suite de + de 2 nombres ne doit pas contenir un 7P car il donnera un 8I et bouclera sur 7P8I etc
Etant la seule boucle qui alterne Pair et Impair avec 2 éléments on doit passer à des boucles de 3 éléments ou + et donc exclure 7P et 8I
Boucles possibles : 7P8I
---
Le seul moyen d'accèder à 5 est par un 1P, donc 5P n'est pas disponible
Possibilités restantes : 1I 2I 4I 5I 7I 1P 2P 4P 8P
Donc 5I mènera forcément à 7P, or ce n'est pas une boucle valable donc on supprime 5I
Si on supprime 5I et 5P il faut supprimer 1P qui était le seul chemin qui y menaitPossibilités restantes : 1I 2I 4I 7I 2P 4P 8P
Pour avoir un 8P il faut un 7P or ce n'est pas possible 2P à la suite
Possibilités restantes : 1I 2I 4I 7I 2P 4P
La suite 2I 7I n'est pas possible
Possibilités restantes : 1I 4I 2P 4P
4I ne peut pas boucler sur lui même car seul chemin venant vers 4 et 1I
Possibilités restantes : 1I 2P 4P
Nous avons donc que 2 boucles possibles
1 à 2 éléments : 7P 8I
1 à 3 éléments : 1I 2P 4POr selon forumeur vinsmock il est impossible d'alterner infiniment entre pair et impair
Comme une boucle pair impair est impossible le nombre diminuera forcément et donc tendra vers 4P 2P 1I
De ce que j'en ai vu, ça m'a l'air faux dès le début avec l'ensemble de travail, puis brouillon avec ton système de notation et ton schéma, ça ne mène pas à grand chose... désolé. 
Surtout que là tu n'as absolument pas généralisé. 
Le 15 avril 2020 à 18:21:27 RoiLoutre5 a écrit :
Le 15 avril 2020 à 18:15:52 Doujinologue a écrit :
Tout d'abord j'étudie la suite dans la définition [0;+inf[ sans le zéroOn sait qu'un nombre pair est divisé par 2 et qu'un nombre impair multiplié par 3 et +1
Je simplifie la suite de la manière suivante : nous ne travaillerons qu'avec la somme digitale de chaque nombre et résultat
On dresse le tableau suivant en fonction de la parité du nombre départ et de sa somme digitale
Le nombre digital parent est en gras et le nombre digital enfant est souligné1/2 = 0,5
5
1*3+1 = 42/2 = 1
2*3+1 = 73/2 = 1,5
6
3*3+1 = 101
4/2 = 2
4*3+1 = 134
5/2 = 2,5
7
5*3+1 = 167
6/2 = 3
6*3+1 = 1910
1
7/2 = 3,5
8
7*3+1 = 224
8/2 = 4
8*3+1 = 257
9/2 = 4,5
9
9*3+1 = 2810
1
On peut dresser l'a figure suivante où grâce à ça
- Les chiffres représentent la somme digitale du nombre X
- Les flèches désignent quelle opération l'ont fait du nombre X (Flèche bleu/2) ( Flèche rouge
*3+1)
Ainsi nous voyons que peu importe le nombre de départ on peut atteindre chaque étape et donc tous les nombres sont liés entre eux mais on voit 3 exceptions :
Propiété 1 : Si on ne commence pas par un nombre dont la somme digitale est de 3 6 ou 9 il sera impossible d'en avoir (représenté par les flèches à sens unique)
Proprité 2: On sait aussi que si le nombre X est impair alors le prochain calcul donnera forcément un nombre pair donc flèche rouge
Avec la Propriété2 il ne peut donc pas avoir 2 opérations impairs à la suite
Donc le nombre X aura qu'un nombre égal d'étapes et devra alterner pair et impair pour boucler, car s'il y a que des opérations pairs ou plus d'opérations pair qu'impaire, il tendra vers 1 donc la boucle 4 2 1
Il faut trouver des boucles qui boucles comme : IP , IPIP, IPIPIP etc..
Comme les 9I 6I 3I sont à sens uniques et bouclent sur du pair elles vont tendre vers 1
On doit qu'utiliser les 1I 2I 4I 5I 7I 8I 1P 2P 4P 5P 7P 8P car elle
dans une suite de + de 2 nombres ne doit pas contenir un 7P car il donnera un 8I et bouclera sur 7P8I etc
Etant la seule boucle qui alterne Pair et Impair avec 2 éléments on doit passer à des boucles de 3 éléments ou + et donc exclure 7P et 8I
Boucles possibles : 7P8I
---
Le seul moyen d'accèder à 5 est par un 1P, donc 5P n'est pas disponible
Possibilités restantes : 1I 2I 4I 5I 7I 1P 2P 4P 8P
Donc 5I mènera forcément à 7P, or ce n'est pas une boucle valable donc on supprime 5I
Si on supprime 5I et 5P il faut supprimer 1P qui était le seul chemin qui y menaitPossibilités restantes : 1I 2I 4I 7I 2P 4P 8P
Pour avoir un 8P il faut un 7P or ce n'est pas possible 2P à la suite
Possibilités restantes : 1I 2I 4I 7I 2P 4P
La suite 2I 7I n'est pas possible
Possibilités restantes : 1I 4I 2P 4P
4I ne peut pas boucler sur lui même car seul chemin venant vers 4 et 1I
Possibilités restantes : 1I 2P 4P
Nous avons donc que 2 boucles possibles
1 à 2 éléments : 7P 8I
1 à 3 éléments : 1I 2P 4POr selon forumeur vinsmock il est impossible d'alterner infiniment entre pair et impair
Comme une boucle pair impair est impossible le nombre diminuera forcément et donc tendra vers 4P 2P 1I
Leur somme digitale de 10 = 1, 11 = 2, 555555 = 30 .gif) 3
3
Le 15 avril 2020 à 18:22:16 Ghauss3 a écrit :
Le 15 avril 2020 à 18:15:52 Doujinologue a écrit :
Tout d'abord j'étudie la suite dans la définition [0;+inf[ sans le zéroOn sait qu'un nombre pair est divisé par 2 et qu'un nombre impair multiplié par 3 et +1
Je simplifie la suite de la manière suivante : nous ne travaillerons qu'avec la somme digitale de chaque nombre et résultat
On dresse le tableau suivant en fonction de la parité du nombre départ et de sa somme digitale
Le nombre digital parent est en gras et le nombre digital enfant est souligné1/2 = 0,5
5
1*3+1 = 42/2 = 1
2*3+1 = 73/2 = 1,5
6
3*3+1 = 101
4/2 = 2
4*3+1 = 134
5/2 = 2,5
7
5*3+1 = 167
6/2 = 3
6*3+1 = 1910
1
7/2 = 3,5
8
7*3+1 = 224
8/2 = 4
8*3+1 = 257
9/2 = 4,5
9
9*3+1 = 2810
1
On peut dresser l'a figure suivante où grâce à ça
- Les chiffres représentent la somme digitale du nombre X
- Les flèches désignent quelle opération l'ont fait du nombre X (Flèche bleu/2) ( Flèche rouge
*3+1)
Ainsi nous voyons que peu importe le nombre de départ on peut atteindre chaque étape et donc tous les nombres sont liés entre eux mais on voit 3 exceptions :
Propiété 1 : Si on ne commence pas par un nombre dont la somme digitale est de 3 6 ou 9 il sera impossible d'en avoir (représenté par les flèches à sens unique)
Proprité 2: On sait aussi que si le nombre X est impair alors le prochain calcul donnera forcément un nombre pair donc flèche rouge
Avec la Propriété2 il ne peut donc pas avoir 2 opérations impairs à la suite
Donc le nombre X aura qu'un nombre égal d'étapes et devra alterner pair et impair pour boucler, car s'il y a que des opérations pairs ou plus d'opérations pair qu'impaire, il tendra vers 1 donc la boucle 4 2 1
Il faut trouver des boucles qui boucles comme : IP , IPIP, IPIPIP etc..
Comme les 9I 6I 3I sont à sens uniques et bouclent sur du pair elles vont tendre vers 1
On doit qu'utiliser les 1I 2I 4I 5I 7I 8I 1P 2P 4P 5P 7P 8P car elle
dans une suite de + de 2 nombres ne doit pas contenir un 7P car il donnera un 8I et bouclera sur 7P8I etc
Etant la seule boucle qui alterne Pair et Impair avec 2 éléments on doit passer à des boucles de 3 éléments ou + et donc exclure 7P et 8I
Boucles possibles : 7P8I
---
Le seul moyen d'accèder à 5 est par un 1P, donc 5P n'est pas disponible
Possibilités restantes : 1I 2I 4I 5I 7I 1P 2P 4P 8P
Donc 5I mènera forcément à 7P, or ce n'est pas une boucle valable donc on supprime 5I
Si on supprime 5I et 5P il faut supprimer 1P qui était le seul chemin qui y menaitPossibilités restantes : 1I 2I 4I 7I 2P 4P 8P
Pour avoir un 8P il faut un 7P or ce n'est pas possible 2P à la suite
Possibilités restantes : 1I 2I 4I 7I 2P 4P
La suite 2I 7I n'est pas possible
Possibilités restantes : 1I 4I 2P 4P
4I ne peut pas boucler sur lui même car seul chemin venant vers 4 et 1I
Possibilités restantes : 1I 2P 4P
Nous avons donc que 2 boucles possibles
1 à 2 éléments : 7P 8I
1 à 3 éléments : 1I 2P 4POr selon forumeur vinsmock il est impossible d'alterner infiniment entre pair et impair
Comme une boucle pair impair est impossible le nombre diminuera forcément et donc tendra vers 4P 2P 1I
De ce que j'en ai vu, ça m'a l'air faux dès le début avec l'ensemble de travail, puis brouillon avec ton système de notation et ton schéma, ça ne mène pas à grand chose... désolé.
Surtout que là tu n'as absolument pas généralisé.
Comment ça généraliser? Fallait juste démontrer que ça tend vers 4 2 1 
Le 15 avril 2020 à 18:15:52 Doujinologue a écrit :
Tout d'abord j'étudie la suite dans la définition [0;+inf[ sans le zéroOn sait qu'un nombre pair est divisé par 2 et qu'un nombre impair multiplié par 3 et +1
Je simplifie la suite de la manière suivante : nous ne travaillerons qu'avec la somme digitale de chaque nombre et résultat
On dresse le tableau suivant en fonction de la parité du nombre départ et de sa somme digitale
Le nombre digital parent est en gras et le nombre digital enfant est souligné1/2 = 0,5
5
1*3+1 = 42/2 = 1
2*3+1 = 73/2 = 1,5
6
3*3+1 = 101
4/2 = 2
4*3+1 = 134
5/2 = 2,5
7
5*3+1 = 167
6/2 = 3
6*3+1 = 1910
1
7/2 = 3,5
8
7*3+1 = 224
8/2 = 4
8*3+1 = 257
9/2 = 4,5
9
9*3+1 = 2810
1
On peut dresser l'a figure suivante où grâce à ça
- Les chiffres représentent la somme digitale du nombre X
- Les flèches désignent quelle opération l'ont fait du nombre X (Flèche bleu/2) ( Flèche rouge
*3+1)
Ainsi nous voyons que peu importe le nombre de départ on peut atteindre chaque étape et donc tous les nombres sont liés entre eux mais on voit 3 exceptions :
Propiété 1 : Si on ne commence pas par un nombre dont la somme digitale est de 3 6 ou 9 il sera impossible d'en avoir (représenté par les flèches à sens unique)
Proprité 2: On sait aussi que si le nombre X est impair alors le prochain calcul donnera forcément un nombre pair donc flèche rouge
Avec la Propriété2 il ne peut donc pas avoir 2 opérations impairs à la suite
Donc le nombre X aura qu'un nombre égal d'étapes et devra alterner pair et impair pour boucler, car s'il y a que des opérations pairs ou plus d'opérations pair qu'impaire, il tendra vers 1 donc la boucle 4 2 1
Il faut trouver des boucles qui boucles comme : IP , IPIP, IPIPIP etc..
Comme les 9I 6I 3I sont à sens uniques et bouclent sur du pair elles vont tendre vers 1
On doit qu'utiliser les 1I 2I 4I 5I 7I 8I 1P 2P 4P 5P 7P 8P car elle
dans une suite de + de 2 nombres ne doit pas contenir un 7P car il donnera un 8I et bouclera sur 7P8I etc
Etant la seule boucle qui alterne Pair et Impair avec 2 éléments on doit passer à des boucles de 3 éléments ou + et donc exclure 7P et 8I
Boucles possibles : 7P8I
---
Le seul moyen d'accèder à 5 est par un 1P, donc 5P n'est pas disponible
Possibilités restantes : 1I 2I 4I 5I 7I 1P 2P 4P 8P
Donc 5I mènera forcément à 7P, or ce n'est pas une boucle valable donc on supprime 5I
Si on supprime 5I et 5P il faut supprimer 1P qui était le seul chemin qui y menaitPossibilités restantes : 1I 2I 4I 7I 2P 4P 8P
Pour avoir un 8P il faut un 7P or ce n'est pas possible 2P à la suite
Possibilités restantes : 1I 2I 4I 7I 2P 4P
La suite 2I 7I n'est pas possible
Possibilités restantes : 1I 4I 2P 4P
4I ne peut pas boucler sur lui même car seul chemin venant vers 4 et 1I
Possibilités restantes : 1I 2P 4P
Nous avons donc que 2 boucles possibles
1 à 2 éléments : 7P 8I
1 à 3 éléments : 1I 2P 4POr selon forumeur vinsmock il est impossible d'alterner infiniment entre pair et impair
Comme une boucle pair impair est impossible le nombre diminuera forcément et donc tendra vers 4P 2P 1I
Meme pas besoin de lire pour savoir que c'est de la merde,
des millier de chercheur bac + 8 avec 30 ans de recherche on jamais réussi, et ici, avec 2 desco, on arrive a trouver la démo en 24h
Données du topic
- Auteur
- Otheocir
- Date de création
- 14 avril 2020 à 23:59:03
- Nb. messages archivés
- 1507
- Nb. messages JVC
- 1507