[MATHS] Pensez-vous qu'à nous tous nous puissions résoudre la conjecture de Syracuse ?
Le 15 avril 2020 à 23:12:06 Lashgar a écrit :
Le 15 avril 2020 à 23:06:34 Otheocir a écrit :
Le 15 avril 2020 à 22:58:48 Yang_Mill a écrit :
Le 15 avril 2020 à 22:42:57 Otheocir a écrit :
Le 15 avril 2020 à 22:36:15 Yang_Mill a écrit :
Le 15 avril 2020 à 22:31:53 Otheocir a écrit :
Le 15 avril 2020 à 22:30:04 Doujinologue a écrit :
Comment on obtient Un+1 si on a besoin de Un+1?non mais j'ai bien refait l'équation en format image regarde ; tu as U(n+1) en fonction de (Un)
Avez-vous tracé la fonction f(x) correspondante estimé confrère ?

J'entends la fonction f telle que u_{n+1} = f(u_n)Je me suis permis de le plotter moi-même cher camarade

Voici un plot sur les 10 premiers termes
un plot sur 100 
et un sur 1,000,000 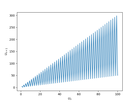

Assurément une avancée fondamentale
Le 15 avril 2020 à 22:58:48 Yang_Mill a écrit :
Le 15 avril 2020 à 22:42:57 Otheocir a écrit :
Le 15 avril 2020 à 22:36:15 Yang_Mill a écrit :
Le 15 avril 2020 à 22:31:53 Otheocir a écrit :
Le 15 avril 2020 à 22:30:04 Doujinologue a écrit :
Comment on obtient Un+1 si on a besoin de Un+1?non mais j'ai bien refait l'équation en format image regarde ; tu as U(n+1) en fonction de (Un)
Avez-vous tracé la fonction f(x) correspondante estimé confrère ?

J'entends la fonction f telle que u_{n+1} = f(u_n)Je me suis permis de le plotter moi-même cher camarade

Voici un plot sur les 10 premiers termes
un plot sur 100 
et un sur 1,000,000 

Assurément une avancée fondamentale
Oui d'où l'inutilité d'une telle équation je sais bien ; si Un pair on descend, si Un impair on monte ;
mais ça je le sais, l'idée c'est que ça nous serve pour l'étape supérieure ;
L'étape supérieure est d'exprimer la fonction Vn = U(n) + U(n-1) + U(n-2) et de montrer que Vn tend vers 7.Démontrer que V tends vers 7 = démontrer que U tends vers le cycle 1, 2, 4.
V dépend de U0 donc impossible de démontrer sa convergence sans démontrer la conjoncture!
oui mais l'un est peut-être plus facile que l'autre à démontrer
Le 15 avril 2020 à 23:13:00 Doujinologue a écrit :
Mais vous faites comment dans les cas où il y a pas 7?
bah si on prouve que ça tend vers 7 CQFD ; si on n'y arrive pas on peut rien conclure, ça reste ptet vrai ou c ptet faux
Le 15 avril 2020 à 23:13:30 Otheocir a écrit :
Le 15 avril 2020 à 23:12:06 Lashgar a écrit :
Le 15 avril 2020 à 23:06:34 Otheocir a écrit :
Le 15 avril 2020 à 22:58:48 Yang_Mill a écrit :
Le 15 avril 2020 à 22:42:57 Otheocir a écrit :
Le 15 avril 2020 à 22:36:15 Yang_Mill a écrit :
Le 15 avril 2020 à 22:31:53 Otheocir a écrit :
Le 15 avril 2020 à 22:30:04 Doujinologue a écrit :
Comment on obtient Un+1 si on a besoin de Un+1?non mais j'ai bien refait l'équation en format image regarde ; tu as U(n+1) en fonction de (Un)
Avez-vous tracé la fonction f(x) correspondante estimé confrère ?

J'entends la fonction f telle que u_{n+1} = f(u_n)Je me suis permis de le plotter moi-même cher camarade

Voici un plot sur les 10 premiers termes
un plot sur 100 
et un sur 1,000,000 

Assurément une avancée fondamentale
Le 15 avril 2020 à 22:58:48 Yang_Mill a écrit :
Le 15 avril 2020 à 22:42:57 Otheocir a écrit :
Le 15 avril 2020 à 22:36:15 Yang_Mill a écrit :
Le 15 avril 2020 à 22:31:53 Otheocir a écrit :
Le 15 avril 2020 à 22:30:04 Doujinologue a écrit :
Comment on obtient Un+1 si on a besoin de Un+1?non mais j'ai bien refait l'équation en format image regarde ; tu as U(n+1) en fonction de (Un)
Avez-vous tracé la fonction f(x) correspondante estimé confrère ?

J'entends la fonction f telle que u_{n+1} = f(u_n)Je me suis permis de le plotter moi-même cher camarade

Voici un plot sur les 10 premiers termes
un plot sur 100 
et un sur 1,000,000 

Assurément une avancée fondamentale
Oui d'où l'inutilité d'une telle équation je sais bien ; si Un pair on descend, si Un impair on monte ;
mais ça je le sais, l'idée c'est que ça nous serve pour l'étape supérieure ;
L'étape supérieure est d'exprimer la fonction Vn = U(n) + U(n-1) + U(n-2) et de montrer que Vn tend vers 7.Démontrer que V tends vers 7 = démontrer que U tends vers le cycle 1, 2, 4.
V dépend de U0 donc impossible de démontrer sa convergence sans démontrer la conjoncture!oui mais l'un est peut-être plus facile que l'autre à démontrer
Possible mais la difficulté de cette suite c'est qu'elle dépend de son premier terme, donc impossible d'exprimer un terme en fonction des autres sans condition, donc il faut parcourir toute l'ensemble des entiers pour démontrer une convergence
Le 15 avril 2020 à 23:14:38 Otheocir a écrit :
Le 15 avril 2020 à 23:13:00 Doujinologue a écrit :
Mais vous faites comment dans les cas où il y a pas 7?bah si on prouve que ça tend vers 7 CQFD ; si on n'y arrive pas on peut rien conclure, ça reste ptet vrai ou c ptet faux
Mais ça tend pas vers 7
Le 15 avril 2020 à 23:06:34 Otheocir a écrit :
Le 15 avril 2020 à 22:58:48 Yang_Mill a écrit :
Le 15 avril 2020 à 22:42:57 Otheocir a écrit :
Le 15 avril 2020 à 22:36:15 Yang_Mill a écrit :
Le 15 avril 2020 à 22:31:53 Otheocir a écrit :
Le 15 avril 2020 à 22:30:04 Doujinologue a écrit :
Comment on obtient Un+1 si on a besoin de Un+1?non mais j'ai bien refait l'équation en format image regarde ; tu as U(n+1) en fonction de (Un)
Avez-vous tracé la fonction f(x) correspondante estimé confrère ? https://image.noelshack.com/fichiers/2019/25/3/1560951106-1545785057-cr7-miroir.png
J'entends la fonction f telle que u_{n+1} = f(u_n)https://www.wolframalpha.com/input/?i=f%28x%29%3D%281-%28-1%29%5E%28x%2B1%29%29%2F2+*+x%2F2+%2B+%281-%28-1%29%5E%28x%29%29%2F2*%283*x%2B1%29
Je me suis permis de le plotter moi-même cher camarade https://image.noelshack.com/fichiers/2019/25/3/1560951106-1545785057-cr7-miroir.png
Voici un plot sur les 10 premiers termes
http://www.noelshack.com/2020-16-3-1586984178-syracusezoom.png un plot sur 100http://www.noelshack.com/2020-16-3-1586984258-syracuse100.png et un sur 1,000,000http://www.noelshack.com/2020-16-3-1586984305-syracuse.png
Assurément une avancée fondamentale https://image.noelshack.com/fichiers/2018/05/1/1517233081-math.pngOui d'où l'inutilité d'une telle équation je sais bien ; si Un pair on descend, si Un impair on monte ;
mais ça je le sais, l'idée c'est que ça nous serve pour l'étape supérieure ;
L'étape supérieure est d'exprimer la fonction Vn = U(n) + U(n-1) + U(n-2) et de montrer que Vn tend vers 7.
Si je puis me permettre de vous aiguiller cher confrère cette approche est déjà utilisé par Chamberland en 1996
Cependant celui ci utilise une expression explicite de la suite légèrement moins, disons directe via u_n+1=f(u_n) où
- f(x) = x/2 cos(x * π/2) ** 2 + (3x+1) sin(x * π/2) ** 2
J'ai bien peur que cette fonction soit plus facile que la votre étant donné qu'elle est définie pour tous réels voire complexes https://image.noelshack.com/fichiers/2019/25/3/1560951106-1545785057-cr7-miroir.png
Le 15 avril 2020 à 23:18:14 Yang_Mill a écrit :
Le 15 avril 2020 à 23:06:34 Otheocir a écrit :
Le 15 avril 2020 à 22:58:48 Yang_Mill a écrit :
Le 15 avril 2020 à 22:42:57 Otheocir a écrit :
Le 15 avril 2020 à 22:36:15 Yang_Mill a écrit :
Le 15 avril 2020 à 22:31:53 Otheocir a écrit :
Le 15 avril 2020 à 22:30:04 Doujinologue a écrit :
Comment on obtient Un+1 si on a besoin de Un+1?non mais j'ai bien refait l'équation en format image regarde ; tu as U(n+1) en fonction de (Un)
Avez-vous tracé la fonction f(x) correspondante estimé confrère ?

J'entends la fonction f telle que u_{n+1} = f(u_n)Je me suis permis de le plotter moi-même cher camarade

Voici un plot sur les 10 premiers termes
un plot sur 100 
et un sur 1,000,000 

Assurément une avancée fondamentale
Oui d'où l'inutilité d'une telle équation je sais bien ; si Un pair on descend, si Un impair on monte ;
mais ça je le sais, l'idée c'est que ça nous serve pour l'étape supérieure ;
L'étape supérieure est d'exprimer la fonction Vn = U(n) + U(n-1) + U(n-2) et de montrer que Vn tend vers 7.Si je puis me permettre de vous aiguiller cher confrère cette approche est déjà utilisé par Chamberland en 1996
https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&cad=rja&uact=8&ved=2ahUKEwjugNjPrOvoAhWJ4J4KHVadAFwQFjAAegQIARAB&url=http%3A%2F%2Fwww.math.grinnell.edu%2F~chamberl%2Fpapers%2F3x_survey_eng.pdf&usg=AOvVaw2n6lv787e_gObyTFUcerKF 
Cependant celui ci utilise une expression explicite de la suite légèrement moins, disons directe via u_n+1=f(u_n) où
- f(x) = x/2 cos(x * π/2) ** 2 + (3x+1) sin(x * π/2) ** 2
J'ai bien peur que cette fonction soit plus facile que la votre étant donné qu'elle est définie pour tous réels voire complexes

Le 15 avril 2020 à 23:17:20 Lashgar a écrit :
Le 15 avril 2020 à 23:13:30 Otheocir a écrit :
Le 15 avril 2020 à 23:12:06 Lashgar a écrit :
Le 15 avril 2020 à 23:06:34 Otheocir a écrit :
Le 15 avril 2020 à 22:58:48 Yang_Mill a écrit :
Le 15 avril 2020 à 22:42:57 Otheocir a écrit :
Le 15 avril 2020 à 22:36:15 Yang_Mill a écrit :
Le 15 avril 2020 à 22:31:53 Otheocir a écrit :
Le 15 avril 2020 à 22:30:04 Doujinologue a écrit :
Comment on obtient Un+1 si on a besoin de Un+1?non mais j'ai bien refait l'équation en format image regarde ; tu as U(n+1) en fonction de (Un)
Avez-vous tracé la fonction f(x) correspondante estimé confrère ?

J'entends la fonction f telle que u_{n+1} = f(u_n)Je me suis permis de le plotter moi-même cher camarade

Voici un plot sur les 10 premiers termes
un plot sur 100 
et un sur 1,000,000 

Assurément une avancée fondamentale
Le 15 avril 2020 à 22:58:48 Yang_Mill a écrit :
Le 15 avril 2020 à 22:42:57 Otheocir a écrit :
Le 15 avril 2020 à 22:36:15 Yang_Mill a écrit :
Le 15 avril 2020 à 22:31:53 Otheocir a écrit :
Le 15 avril 2020 à 22:30:04 Doujinologue a écrit :
Comment on obtient Un+1 si on a besoin de Un+1?non mais j'ai bien refait l'équation en format image regarde ; tu as U(n+1) en fonction de (Un)
Avez-vous tracé la fonction f(x) correspondante estimé confrère ?

J'entends la fonction f telle que u_{n+1} = f(u_n)Je me suis permis de le plotter moi-même cher camarade

Voici un plot sur les 10 premiers termes
un plot sur 100 
et un sur 1,000,000 

Assurément une avancée fondamentale
Oui d'où l'inutilité d'une telle équation je sais bien ; si Un pair on descend, si Un impair on monte ;
mais ça je le sais, l'idée c'est que ça nous serve pour l'étape supérieure ;
L'étape supérieure est d'exprimer la fonction Vn = U(n) + U(n-1) + U(n-2) et de montrer que Vn tend vers 7.Démontrer que V tends vers 7 = démontrer que U tends vers le cycle 1, 2, 4.
V dépend de U0 donc impossible de démontrer sa convergence sans démontrer la conjoncture!oui mais l'un est peut-être plus facile que l'autre à démontrer
Possible mais la difficulté de cette suite c'est qu'elle dépend de son premier terme, donc impossible d'exprimer un terme en fonction des autres sans condition, donc il faut parcourir toute l'ensemble des entiers pour démontrer une convergence
Oui c'est fort possible ;
Mais si on arrive à exprimer Vn (telle que définie) en fonction de Un-1 seulement (sans l'exprimer en fonction du premier terme) et qu'on en tire une propriété quelconque montrant qu’elle tend vers 7 quelque soit Un-1 ça devrait le faire ; mais il faut que je développe sur papier j'ai pas eu le temps.
Le 15 avril 2020 à 23:18:14 Yang_Mill a écrit :
Le 15 avril 2020 à 23:06:34 Otheocir a écrit :
Le 15 avril 2020 à 22:58:48 Yang_Mill a écrit :
Le 15 avril 2020 à 22:42:57 Otheocir a écrit :
Le 15 avril 2020 à 22:36:15 Yang_Mill a écrit :
Le 15 avril 2020 à 22:31:53 Otheocir a écrit :
Le 15 avril 2020 à 22:30:04 Doujinologue a écrit :
Comment on obtient Un+1 si on a besoin de Un+1?non mais j'ai bien refait l'équation en format image regarde ; tu as U(n+1) en fonction de (Un)
Avez-vous tracé la fonction f(x) correspondante estimé confrère ?

J'entends la fonction f telle que u_{n+1} = f(u_n)Je me suis permis de le plotter moi-même cher camarade

Voici un plot sur les 10 premiers termes
un plot sur 100 
et un sur 1,000,000 

Assurément une avancée fondamentale
Oui d'où l'inutilité d'une telle équation je sais bien ; si Un pair on descend, si Un impair on monte ;
mais ça je le sais, l'idée c'est que ça nous serve pour l'étape supérieure ;
L'étape supérieure est d'exprimer la fonction Vn = U(n) + U(n-1) + U(n-2) et de montrer que Vn tend vers 7.Si je puis me permettre de vous aiguiller cher confrère cette approche est déjà utilisé par Chamberland en 1996
https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&cad=rja&uact=8&ved=2ahUKEwjugNjPrOvoAhWJ4J4KHVadAFwQFjAAegQIARAB&url=http%3A%2F%2Fwww.math.grinnell.edu%2F~chamberl%2Fpapers%2F3x_survey_eng.pdf&usg=AOvVaw2n6lv787e_gObyTFUcerKF 
Cependant celui ci utilise une expression explicite de la suite légèrement moins, disons directe via u_n+1=f(u_n) où
- f(x) = x/2 cos(x * π/2) ** 2 + (3x+1) sin(x * π/2) ** 2
J'ai bien peur que cette fonction soit plus facile que la votre étant donné qu'elle est définie pour tous réels voire complexes

dis nous de suite qu'on est dans une impasse tant que tu y es .gif)
N’empêche on a le même chemin que les pro c'est balèze tu avoueras 

Il faut voir plus haut
Le 15 avril 2020 à 23:17:52 Doujinologue a écrit :
Le 15 avril 2020 à 23:14:38 Otheocir a écrit :
Le 15 avril 2020 à 23:13:00 Doujinologue a écrit :
Mais vous faites comment dans les cas où il y a pas 7?bah si on prouve que ça tend vers 7 CQFD ; si on n'y arrive pas on peut rien conclure, ça reste ptet vrai ou c ptet faux
Mais ça tend pas vers 7
Qu'et-ce que tu en sais ?
Le 15 avril 2020 à 23:26:34 Otheocir a écrit :
Le 15 avril 2020 à 23:17:52 Doujinologue a écrit :
Le 15 avril 2020 à 23:14:38 Otheocir a écrit :
Le 15 avril 2020 à 23:13:00 Doujinologue a écrit :
Mais vous faites comment dans les cas où il y a pas 7?bah si on prouve que ça tend vers 7 CQFD ; si on n'y arrive pas on peut rien conclure, ça reste ptet vrai ou c ptet faux
Mais ça tend pas vers 7
Qu'et-ce que tu en sais ?
avec 2048 tu fais quoi?
Le 15 avril 2020 à 23:27:32 Doujinologue a écrit :
Le 15 avril 2020 à 23:26:34 Otheocir a écrit :
Le 15 avril 2020 à 23:17:52 Doujinologue a écrit :
Le 15 avril 2020 à 23:14:38 Otheocir a écrit :
Le 15 avril 2020 à 23:13:00 Doujinologue a écrit :
Mais vous faites comment dans les cas où il y a pas 7?bah si on prouve que ça tend vers 7 CQFD ; si on n'y arrive pas on peut rien conclure, ça reste ptet vrai ou c ptet faux
Mais ça tend pas vers 7
Qu'et-ce que tu en sais ?
avec 2048 tu fais quoi?
je code un algo et l'algo me dit
2048 est un petit nombre, donc il a déjà été testé donc la suite tend vers 7
[23:27:32] <Doujinologue>
Le 15 avril 2020 à 23:26:34 Otheocir a écrit :
Le 15 avril 2020 à 23:17:52 Doujinologue a écrit :
Le 15 avril 2020 à 23:14:38 Otheocir a écrit :
Le 15 avril 2020 à 23:13:00 Doujinologue a écrit :
Mais vous faites comment dans les cas où il y a pas 7?bah si on prouve que ça tend vers 7 CQFD ; si on n'y arrive pas on peut rien conclure, ça reste ptet vrai ou c ptet faux
Mais ça tend pas vers 7
Qu'et-ce que tu en sais ?
avec 2048 tu fais quoi?
Bah 2048=2^11 donc tu divises par 2 jusqu'à arriver au cycle 4 2 1
Le 15 avril 2020 à 23:28:22 Otheocir a écrit :
Le 15 avril 2020 à 23:27:32 Doujinologue a écrit :
Le 15 avril 2020 à 23:26:34 Otheocir a écrit :
Le 15 avril 2020 à 23:17:52 Doujinologue a écrit :
Le 15 avril 2020 à 23:14:38 Otheocir a écrit :
Le 15 avril 2020 à 23:13:00 Doujinologue a écrit :
Mais vous faites comment dans les cas où il y a pas 7?bah si on prouve que ça tend vers 7 CQFD ; si on n'y arrive pas on peut rien conclure, ça reste ptet vrai ou c ptet faux
Mais ça tend pas vers 7
Qu'et-ce que tu en sais ?
avec 2048 tu fais quoi?
je code un algo et l'algo me dit
2048 ça tend pas vers 7
Le 15 avril 2020 à 23:29:04 Doujinologue a écrit :
Le 15 avril 2020 à 23:28:22 Otheocir a écrit :
Le 15 avril 2020 à 23:27:32 Doujinologue a écrit :
Le 15 avril 2020 à 23:26:34 Otheocir a écrit :
Le 15 avril 2020 à 23:17:52 Doujinologue a écrit :
Le 15 avril 2020 à 23:14:38 Otheocir a écrit :
Le 15 avril 2020 à 23:13:00 Doujinologue a écrit :
Mais vous faites comment dans les cas où il y a pas 7?bah si on prouve que ça tend vers 7 CQFD ; si on n'y arrive pas on peut rien conclure, ça reste ptet vrai ou c ptet faux
Mais ça tend pas vers 7
Qu'et-ce que tu en sais ?
avec 2048 tu fais quoi?
je code un algo et l'algo me dit
2048 ça tend pas vers 7
non mais Vn tend vers 7 pas Un
Le 15 avril 2020 à 23:29:45 Otheocir a écrit :
Le 15 avril 2020 à 23:29:04 Doujinologue a écrit :
Le 15 avril 2020 à 23:28:22 Otheocir a écrit :
Le 15 avril 2020 à 23:27:32 Doujinologue a écrit :
Le 15 avril 2020 à 23:26:34 Otheocir a écrit :
Le 15 avril 2020 à 23:17:52 Doujinologue a écrit :
Le 15 avril 2020 à 23:14:38 Otheocir a écrit :
Le 15 avril 2020 à 23:13:00 Doujinologue a écrit :
Mais vous faites comment dans les cas où il y a pas 7?bah si on prouve que ça tend vers 7 CQFD ; si on n'y arrive pas on peut rien conclure, ça reste ptet vrai ou c ptet faux
Mais ça tend pas vers 7
Qu'et-ce que tu en sais ?
avec 2048 tu fais quoi?
je code un algo et l'algo me dit
2048 ça tend pas vers 7
non mais Vn tend vers 7 pas Un
Ah c'est quoi Vn?
Le 15 avril 2020 à 23:30:03 Doujinologue a écrit :
Le 15 avril 2020 à 23:29:45 Otheocir a écrit :
Le 15 avril 2020 à 23:29:04 Doujinologue a écrit :
Le 15 avril 2020 à 23:28:22 Otheocir a écrit :
Le 15 avril 2020 à 23:27:32 Doujinologue a écrit :
Le 15 avril 2020 à 23:26:34 Otheocir a écrit :
Le 15 avril 2020 à 23:17:52 Doujinologue a écrit :
Le 15 avril 2020 à 23:14:38 Otheocir a écrit :
Le 15 avril 2020 à 23:13:00 Doujinologue a écrit :
Mais vous faites comment dans les cas où il y a pas 7?bah si on prouve que ça tend vers 7 CQFD ; si on n'y arrive pas on peut rien conclure, ça reste ptet vrai ou c ptet faux
Mais ça tend pas vers 7
Qu'et-ce que tu en sais ?
avec 2048 tu fais quoi?
je code un algo et l'algo me dit
2048 ça tend pas vers 7
non mais Vn tend vers 7 pas Un
Ah c'est quoi Vn?
Vn c'est la somme de trois termes consécutifs, faut suivre
Le 15 avril 2020 à 23:26:15 Otheocir a écrit :
Et le problème avec les cosinus c'est qu'on arrive à rien ; OK on a posé cos ou sin mais après ?
Il faut voir plus haut
Mon honoré confrère il me semble que votre affirmation soit un peu rapide 
Wikipédia est formel sur le fait qu'à l'aide de cette fonction et en l'étudiant sur le plan réel Chamberland a pu montrer que la conjecture était fausse sur les réels et mettre en évidence un nouveau cycle 1,1925 - 2,1386 
De plus en l'étudiant sur le plan complexe on obtient cette figure ma foi fort sympathique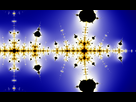

Données du topic
- Auteur
- Otheocir
- Date de création
- 14 avril 2020 à 21:59:03
- Nb. messages archivés
- 1507
- Nb. messages JVC
- 1507
