[Maths] Docteur en maths pures, posez vos questions

J'up, le sujet m'intéresse et c'est un peu ce à quoi j'aspire (idéalement)

• A partir de quel moment tu t'es dit que tel domaine des maths t'intéressait le plus, ou alors que tel domaine des math était celui où tu avais le plus d'intuition? Lycée, prepa, ou après?

• Maîtrisais-tu quelques notions du programme du supérieur au lycée? Tu dis que tu as "passé un cap en prepa". Tu veux dire que la maîtrise des notions abstraites qu'on voit en prepa t'es apparue qu'en prepa, et qu'avant tu n'arrivais pas à raisonner sur des objets "abstraits" par rapport au lycée (algèbre notamment)?

• Ton classement au CG et aux olympiades?

• Des problèmes ou des notions qui t'ont traumatisés, sur lesquels tu as longtemps séché?

Le 19 mai 2019 à 13:35:24 Stanton_Dowd a écrit :
Tu as fini ta thèse à quel âge ? A quel point dans ton parcours est-ce que tu t'es dit "C'est bon, j'ai une vraie maîtrise de mon domaine de recherche" (si c'est arrivé un jour) ?
Est-ce que des fois tu angoisses de ne pas connaître des concepts/techniques de preuve d'un autre domaine que le tien mais qui pourraient t'aider à résoudre les problèmes auxquels tu es confronté ?

A 26 ans. Je saurais pas dire exactement, en tout cas, j'avais pas l'impression de maîtriser encore mon domaine à la fin de ma thèse (en dehors du cercle très étroit de mes travaux), maintenant après les postdocs je me sens plus mûr et polyvalent, mais on doit apprendre de nouvelles choses sans cesse
Angoisser n'est pas le bon terme; être frustré quand une réponse semble accessible mais qu'il nous manque un outil ça peut arriver Dans ce cas, il faut en discuter autour de soi et garder le problème en tête pour plus tard.

Le 19 mai 2019 à 13:47:15 mcgardelapeche a écrit :
Tu maîtrise bien Latex je suppose ? Des conseils pour progresser dessus ?

Ca va, je fais pas des trucs de ouf avec mais je maîtrise ce dont j'ai besoin. Pas de conseil particulier, tu peux suivre un tuto comme celui-là:
https://www.tuteurs.ens.fr/logiciels/latex/
Utilise le tuto pour avancer simultanément sur ton projet, c'est comme ça qu'on apprend.

Le 19 mai 2019 à 23:22:47 Phimosin a écrit :
J'up, le sujet m'intéresse et c'est un peu ce à quoi j'aspire (idéalement)

• A partir de quel moment tu t'es dit que tel domaine des maths t'intéressait le plus, ou alors que tel domaine des math était celui où tu avais le plus d'intuition? Lycée, prepa, ou après?

En prépa déjà j'avais beaucoup aimé la topologie, mais l'algèbre me plaisait beaucoup aussi...Jusqu'en fin de M1 j'ai continué à suivre des cours très variés, je me suis décidé pour la topologie parce qu'elle peut faire appel à toutes les autres branches des maths, et à cause d'un excellent prof que j'ai eu en L3/M1.

• Maîtrisais-tu quelques notions du programme du supérieur au lycée? Tu dis que tu as "passé un cap en prepa". Tu veux dire que la maîtrise des notions abstraites qu'on voit en prepa t'es apparue qu'en prepa, et qu'avant tu n'arrivais pas à raisonner sur des objets "abstraits" par rapport au lycée (algèbre notamment)?

Non, je n'avais jamais cherché à m'avancer sur le programme du supérieur au lycée. C'est sans doute pourquoi j'ai eu la sensation de progresser en prépa; faut dire qu'avec les maths du lycée on est vite limité

• Ton classement au CG et aux olympiades?

J'avais participé au CG et aux olympiades académiques mais j'ai pas été classé.

• Des problèmes ou des notions qui t'ont traumatisés, sur lesquels tu as longtemps séché?

Surtout des chapitres de cours un peu rébarbatifs, comme les courbes paramétrées en prépa
Y a eu des problèmes *** en prépa sur lesquels j'ai galéré à l'époque et trouvé la solution des mois après mais je m'en rappelle plus là
Et aussi en thèse, des questions sur lesquelles j'ai buté pendant un an pour finalement trouvé la solution un matin dans mon lit
Mais si tu voulais un exo joli, en voici un:

Le 20 mai 2019 à 02:14:24 Oltruomega11 a écrit :
La primitive de 4x ?

Les primitives, 2x^2+C

Le 20 mai 2019 à 02:13:59 FTM2 a écrit :
Tu bossais combien d'heures par jour en doctorat ? Tu dois incroyablement travailler pour acquérir ce genre de niveau non ?

C'est très variable en fait. Déjà, tu es maître de ton emploi du temps (en dehors des cours) donc tu décides quand tu travailles. Y a différentes phases dans un projet de recherche:
-Une première phase où la direction de ton projet est encore floue et où tu peux avoir du mal à te concentrer longtemps
-La phase jouissive où tu as presque trouvé la solution et tu peux bosser comme un fou jusqu'à en oublier de dormir et manger
-La phase où tu dois rédiger tes résultats, ce qui prend du temps (surtout que tu découvres souvent des petites erreurs dans ton raisonnement ) où il faut bosser régulièrement pour que la rédaction avance.

D'ailleurs je dois m'y remettre

Salut a tous, j'ai lu "Docteur en maths pures, posez vos questions" du coup je tente ma chance, je ne suis pas tres bon en math et j'ai du mal a trouver une solution a mon probleme, le voici :

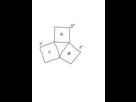
trois carrés forment un cercle dans lequel se trouve un triangle isocèle.
Chacun des carrés est nommé ainsi : A, B & C et tournent sur eux memes pour former ce triangle.
exemple : le carré A est à 0°.

a quel degré les carrés suivant peuvent ils etre tournés pour pouvoir former ce triangle ?

Quel domaine ?

Sinon un exo trivial : trouve des entiers positif non nul tel que x^3 + y^3 = z^3

Le 03 août 2021 à 18:54:15 :
Salut a tous, j'ai lu "Docteur en maths pures, posez vos questions" du coup je tente ma chance, je ne suis pas tres bon en math et j'ai du mal a trouver une solution a mon probleme, le voici :

trois carrés forment un cercle dans lequel se trouve un triangle isocèle.
Chacun des carrés est nommé ainsi : A, B & C et tournent sur eux memes pour former ce triangle.
exemple : le carré A est à 0°.

a quel degré les carrés suivant peuvent ils etre tournés pour pouvoir former ce triangle ?

Ca dépend pas des angles mais des côtés des carrés.

Le 03 août 2021 à 18:54:15 :
Salut a tous, j'ai lu "Docteur en maths pures, posez vos questions" du coup je tente ma chance, je ne suis pas tres bon en math et j'ai du mal a trouver une solution a mon probleme, le voici :

trois carrés forment un cercle dans lequel se trouve un triangle equilateral.
Chacun des carrés est nommé ainsi : A, B & C et tournent sur eux memes pour former ce triangle.
exemple : le carré A est à 0°.

a quel degré les carrés suivant peuvent ils etre tournés pour pouvoir former ce triangle ?

Le 03 août 2021 à 19:36:23 :
les cotés sont equilatérals. apres peu importe leur tailles, disons que chaque cotés des carrés mesures 1cm

si chaque côté mesure 1cm le triangle ne peut être qu'équilatéral. Mais les angles du triangles sont de 60° chacun.

Le 03 août 2021 à 20:05:16 :
Ce silence est éloquent. Tant pis

Le topic date de 2019…

Le 03 août 2021 à 20:09:41 :

Le 03 août 2021 à 20:05:16 :
Ce silence est éloquent. Tant pis

Le topic date de 2019…

ahi j'avais pas vu, merci khey

Le 19 mai 2019 à 00:56:07 :
Si tu as fait du traitement du signal, je comprends pas pourquoi le fait d'echantillonner un signal analogique donne une périodicité spectrale. Genre il y a la fondamentale a 5kHz puis un pic a 10kHz puis un pic tous les n*5kHz

C'est un peu à cause du cosinus digital cos(2*pi*n*f) c'est périodique en n et en f à la fois (pour f rationnel). Une autre démonstration considère que échantilloner consiste à multiplier par un peigne de dirac. Or la transformé de fourier d'un peigne de dirac est encore un peigne de dirac et la multipcation dans le domaine temporel se transforme en convolution dans le domaine fréquentiel. D'ou la périodicité (convolution avec un peigne de dirac)

Le 03 août 2021 à 18:54:41 :
Quel domaine ?

Sinon un exo trivial : trouve des entiers positif non nul tel que x^3 + y^3 = z^3

Topologie.

L'exo trivial c'est le théorème de Fermat-Wiles pour n=3, il n'y a pas de solutions non triviales. Mais pour n=3, c'est faisable: il faut voir qu'on peut travailler dans l'anneau factoriel Z[j] où j est une racine cubique de l'unité. Je te renvoie à https://fr.wikipedia.org/wiki/D%C3%A9monstration_du_dernier_th%C3%A9or%C3%A8me_de_Fermat_pour_les_exposants_3,_4_et_5#Cas_o%C3%B9_n_est_%C3%A9gal_%C3%A0_trois

Tu n'as pas l'impression que ce que tu fais au quotidien est complètement inutile ?
Petit exo :
Soit E un ev de dim finie, K un compact de E d'intérieur non vide, et u un endo de E tel que u(K) inclus dans K. Montre que |det(n)|<= 1 .
( juste donner l'idée de la démo c'est ok )

Si, un peu Après il faut voir ce qu'on appelle utile: d'un côté, je m'attends pas du tout à ce que les problèmes que j'étudie ait des applications industrielles ou autres; d'un autre côté, on peut considérer les maths comme faisant partie de la culture. De fait, les problèmes mathématiques même purement théoriques intéressent beaucoup de monde; il y a beaucoup de fascination pour les maths (toi même tu m'as donné un exo parce que ça t'amuse )
Bref, à titre perso, j'ai un approche assez égoïste: j'aime ce que je fais et tant qu'il y a de la demande pour mon travail de chercheur, je prends sans me poser de question.

Pour l'exo, l'idée est d'utiliser le volume: Vol(u(K))=|det(u)|Vol(K) donc |det(u)|<=1. Le volume de D étant l'intégrale de 1 sur D.