[MATHS] Venez me TESTER ma MÉDIOCRITÉ en POSANT vos QUESTIONS !

Le 10 juillet 2024 à 21:28:24 PanierDeBasket1 a écrit :

Le 10 juillet 2024 à 21:24:41 :

Le 10 juillet 2024 à 21:21:58 PanierDeBasket1 a écrit :
Explique moi le concept de dérivation pourquoi avoir besoin de dérivé

Pour étudier la croissance d'une fonction. Une dérivée positive indique une pente croissante, "la fonction monte". Plus la dérivée est grande, plus la fonction croît rapidement. Inversement une dérivée faible indique que la fonction ne croît presque plus.

Par exemple, pour le logarithme, la dérivée c'est 1/x. La fonction inverse converge très rapidement vers 0. Donc le logarithme est à croissance très lente.

Ok explique moi les nombre complexes à quoi servent t’il

Les nombres complexes sont une formalisation de la géométrie. Tu peux faire de la géométrie avec des points, des vecteurs, des cercles... Mais tu peux aussi faire de la géométrie par le calcul formel, en représentant les points du plan par des nombres "complexes".

Le 10 juillet 2024 à 21:29:58 Tchesnokov a écrit :
C'est quoi le théorème d'incomplétude de Gödel ?

Un théorème plus ou moins inutile de logique, à savoir le domaine des mathématiques le plus incompréhensible et le plus immonde à mon goût. Il sert juste à faire bander les novices sur de la philosophie mathématique. J'ai jamais chercher à comprendre ce théorème ou sa démonstration et je m'en tamponne.

Est-il vrai que tout champ de vecteurs tangents continu sur Sn avec n pair s'annule en au moins un point ?

Si oui, preuve de ce théorème
Sinon contre exemple

C'est pour mon rattrapage de BTS mais je suis pas sur, je pencherais plutôt sur le fait qu'il soit vrai

Le 10 juillet 2024 à 21:35:18 PanierDeBasket1 a écrit :
Une dernière question Pour quoi les nombres premiers sont si intrigants et pourquoi ont-ils une place plus importante dans le paysage Mathématique que le reste des nombres

Parce qu'il y a des énoncés simples dont les démonstrations sont hardcore (par exemple le grand théorème de Fermat) ou inaccessibles à l'heure actuelle (conjectures de Goldbach, nombres premiers jumeaux, etc.).

Le 10 juillet 2024 à 21:36:58 AnotherWorld4 a écrit :
Est-il vrai que tout champ de vecteurs tangents continu sur Sn avec n pair s'annule en au moins un point ?

Si oui, preuve de ce théorème
Sinon contre exemple

C'est pour mon rattrapage de BTS mais je suis pas sur

Alors ça c'est pas du tout niveau BTS
Oui c'est vrai, ça porte même un nom : Le Théorème de la Boule Chevelue.
Je sais pas démontrer ça tout seul.
De mémoire, on peut faire appel à des calculs de volumes sur les variétés différentielles via la formule de Stokes. Mais j'en dis pas plus parce que je vais m'embourber sinon.

Le 10 juillet 2024 à 21:29:48 DonDoritos35 a écrit :
Un exercice de calcul intégral niveau L2
Calculer

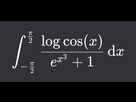
C'est quoi cette immondice ?
Jamais je calcule cette merde moi.

Est-ce que si on coupe en deux [-pi/2,0] et [0,pi/2] et qu'on fait un changement de variable du style t=cos(x) ça marche ?
Ou alors on transforme un truc en son DSE

Le 10 juillet 2024 à 21:43:37 Kim_Jong_H2L a écrit :
Tout Entier Naturel Exponentiel Univers N De Son Avale le départ dès n Supérieur ou égal à 1 se décompose en un Unique Produit De Nombres Premiers. Cette Décomposition est unique à l'ordre des 4 unités 2 ; 3 ; 5 ; 7 Les Facteurs 2 des Quotients successives NP1 ; NP2 ; NP3 ; NP5 ; NP7 Du Grand N = Grand NP9 = 9...99 + 1 puis eux même pour revenir en divisibilité de Son Amont NEU 9- = 9...9,9.9+9,9.9%+9,9.9° = i x 4 = | ( 5 + 7 + ... + ( 9...93 = 0 [3] = NP3 ) = ( NP2 = 9...90 ) ) = 9...90 + ( 3 x 3 = 9 ) + (1 = 1,0.0 = 0,99 999 999 99 ) | + ( 0 = A = espace vide de l'ensemble de base d'un raisonnent pose un volume quelconque linéairement du n supérieur ou égalés à 1 ou son amont des n & grand N = 9 = J la dixième lettres des Alphabets.

Le fameux théorème NEU pour toutes les mathématiques finies dans leurs parties par le Grand Mathématicien AZZAZ l'ATOME

Not ready pour l'ouverture du coffre mathématique

Le 10 juillet 2024 à 21:44:33 MouetteAveugle a écrit :

Le 10 juillet 2024 à 21:29:48 DonDoritos35 a écrit :
Un exercice de calcul intégral niveau L2
Calculer

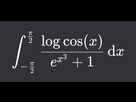
C'est quoi cette immondice ?
Jamais je calcule cette merde moi.

Est-ce que si on coupe en deux [-pi/2,0] et [0,pi/2] et qu'on fait un changement de variable du style t=cos(x) ça marche ?
Ou alors on transforme un truc en son DSE

Oui, c'est un bon point de départ.

Sur quelle base théorique se repose les modèles de réseaux de neurones en IA ?

Nom du théorème + plan de la démonstration

Le 10 juillet 2024 à 21:47:23 :
Les maths, de tout manière pour être bon, il suffit juste de boucler sur les exos.
Jamais compris la hype " bon en maths = génie " .

El famoso

Le 10 juillet 2024 à 21:47:24 AnotherWorld4 a écrit :
Sur quelle base théorique se repose les modèles de réseaux de neurones en IA ?

Nom du théorème + plan de la démonstration

Ça repose principalement sur la théorie de l'algèbre linéaire. J'ai pas de nom de théorème particulier à te donner, ta question a pas trop de sens.

Si ça te fait plaisir je peux te citer le théorème spectral, mais par contre je le démontre pas.

Le 10 juillet 2024 à 21:49:16 :

Le 10 juillet 2024 à 21:47:24 AnotherWorld4 a écrit :
Sur quelle base théorique se repose les modèles de réseaux de neurones en IA ?

Nom du théorème + plan de la démonstration

Ça repose principalement sur la théorie de l'algèbre linéaire. J'ai pas de nom de théorème particulier à te donner, ta question a pas trop de sens.

Si ça te fait plaisir je peux te citer le théorème spectral, mais par contre je le démontre pas.

Non c'était le théorème de représentation de Kolmogorov auquel je pensais

C'était plutôt une question culture G

Le 10 juillet 2024 à 21:47:41 :

Le 10 juillet 2024 à 21:47:23 :
Les maths, de tout manière pour être bon, il suffit juste de boucler sur les exos.
Jamais compris la hype " bon en maths = génie " .

El famoso

Tu verras quand tu feras des maths.
J'avais la meilleure note de ma classe en maths et l'unique raison de cette réussite, c'est le bouclage.

Le 10 juillet 2024 à 21:54:41 :

Le 10 juillet 2024 à 21:47:41 :

Le 10 juillet 2024 à 21:47:23 :
Les maths, de tout manière pour être bon, il suffit juste de boucler sur les exos.
Jamais compris la hype " bon en maths = génie " .

El famoso

Tu verras quand tu feras des maths.
J'avais la meilleure note de ma classe en maths et l'unique raison de cette réussite, c'est le bouclage.

A partir de quand ou quoi considère tu qu'on fais des maths ?

Le 10 juillet 2024 à 21:54:05 AnotherWorld4 a écrit :

Le 10 juillet 2024 à 21:49:16 :

Le 10 juillet 2024 à 21:47:24 AnotherWorld4 a écrit :
Sur quelle base théorique se repose les modèles de réseaux de neurones en IA ?

Nom du théorème + plan de la démonstration

Ça repose principalement sur la théorie de l'algèbre linéaire. J'ai pas de nom de théorème particulier à te donner, ta question a pas trop de sens.

Si ça te fait plaisir je peux te citer le théorème spectral, mais par contre je le démontre pas.

Non c'était le théorème de représentation de Kolmogorov auquel je pensais

C'était plutôt une question culture G

C'est un lemme d'un des problèmes de Hilbert https://en.m.wikipedia.org/wiki/Hilbert%27s_thirteenth_problem

Mouais, ça me parle pas du tout, je fais pas d'IA moi de toute façon