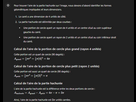
[MATHS] Trouver l'aire de la partie hachurée
[11:56:11] <Taku[Shiny]>
Le 15 juin 2024 à 11:37:26 :
Malheureusement ChatGPT est très mauvais en maths.
c'est si mauvais que ça?
Yep. 
[11:57:17] <TheLelouch4>
Fais un dessin lisible et on te répondra
Le dessin n'a pas besoin d'être lisible, toutes les informations sont sur dessus. 
Le 15 juin 2024 à 11:22:00 :
tu trouves le point où les cercles se croisent puis tu fais deux intégrales
[12:00:23] <dreamonete>
Le 15 juin 2024 à 11:22:00 :
tu trouves le point où les cercles se croisent puis tu fais deux intégrales
Ouais donc tout le monde s'accorde pour dire qu'il faut passer par une double intégrale je suppose. Pas de moyen plus simple vous pensez ? 

J'essaye un truc je reviens.

[12:02:38] <DonDoritos35>
On peut calculer l'aire de ta surface en exploitant les symétries de la figure je crois.
J'essaye un truc je reviens.
Je t'en prie. 

[12:10:08] <parcoursoupe>
c'est entre x = 0.8 et x = 4
Merci clé. 
[12:09:58] <Martin48295>
On additionne les aires des 2 arcs et du triangle courbé à gauche qu'on soustrait de lair totale

Un quart de cercle de rayon 4, un demi-cercle de rayon 2.
Je vais essayer
Alors on suppose que les 3 figures qu'on voit sont : un carré, un demi-cercle et un quart de cercle.
L'air du carré est simple, 4x4= 16.
L'air du quart de cercle, qui a pour rayon 4 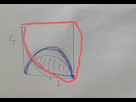 , est :
, est :
(4^(2)×pi)/4 = 12,6 environ
L'air du demi-cercle, qui a pour rayon 2 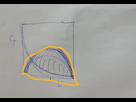 , est (2^(2)×pi)/2 = 6,3 environ
, est (2^(2)×pi)/2 = 6,3 environ
L'air de la partie bleue  est, 16 - 12,6 = 3,4
est, 16 - 12,6 = 3,4
Ensuite... Ensuite je suis perdu
[12:27:50] <Avatar_Zuko>
Un quart de cercle de rayon 4, un demi-cercle de rayon 2.
Je vais essayer
Alors on suppose que les 3 figures qu'on voit sont : un carré, un demi-cercle et un quart de cercle.
L'air du carré est simple, 4x4= 16.
L'air du quart de cercle, qui a pour rayon 4
, est :
(4^(2)×pi)/4 = 12,6 environL'air du demi-cercle, qui a pour rayon 2
, est (2^(2)×pi)/2 = 6,3 environ
L'air de la partie bleue
est, 16 - 12,6 = 3,4
Ensuite... Ensuite je suis perdu
Merci d'avoir tenté clé. 
Le 15 juin 2024 à 12:29:12 :
[12:27:50] <Avatar_Zuko>
Un quart de cercle de rayon 4, un demi-cercle de rayon 2.
Je vais essayer
Alors on suppose que les 3 figures qu'on voit sont : un carré, un demi-cercle et un quart de cercle.
L'air du carré est simple, 4x4= 16.
L'air du quart de cercle, qui a pour rayon 4
, est :
(4^(2)×pi)/4 = 12,6 environL'air du demi-cercle, qui a pour rayon 2
, est (2^(2)×pi)/2 = 6,3 environ
L'air de la partie bleue
est, 16 - 12,6 = 3,4
Ensuite... Ensuite je suis perdu
Merci d'avoir tenté clé.
De... de rien 
[12:30:09] <parcoursoupe>
ça donne 3.85 ton aire avec 2 intégrales
Tu peux détailler un peu grossièrement ou flemme ? 
[12:30:53] <Avatar_Zuko>
Le 15 juin 2024 à 12:29:12 :
[12:27:50] <Avatar_Zuko>
Un quart de cercle de rayon 4, un demi-cercle de rayon 2.
Je vais essayer
Alors on suppose que les 3 figures qu'on voit sont : un carré, un demi-cercle et un quart de cercle.
L'air du carré est simple, 4x4= 16.
L'air du quart de cercle, qui a pour rayon 4
, est :
(4^(2)×pi)/4 = 12,6 environL'air du demi-cercle, qui a pour rayon 2
, est (2^(2)×pi)/2 = 6,3 environ
L'air de la partie bleue
est, 16 - 12,6 = 3,4
Ensuite... Ensuite je suis perdu
Merci d'avoir tenté clé.
De... de rien
Ça va aller va. 
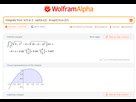
f(x) = 4 - sqrt(16 - (x - 4)²)
g(x) = sqrt(4 - (x - 2)²)
Il a fait les intégrales à ma place entre 0.8 et 4 (car la flemme) et soustrait les 2.
[12:33:01] <parcoursoupe>
Bah j'ai tracé la figure sur Geogebra
f(x) = 4 - sqrt(16 - (x - 4)²)
g(x) = sqrt(4 - (x - 2)²)
Il a fait les intégrales à ma place entre 0.8 et 4 (car la flemme) et soustrait les 2.
Ahi merci, ça fonctionne aussi certes. 
-6/5 c'est la valeur où les courbes se croisent
j'ai centré le graphe sur le petit cercle
Données du topic
- Auteur
- Stalhblume
- Date de création
- 15 juin 2024 à 09:15:08
- Nb. messages archivés
- 60
- Nb. messages JVC
- 60