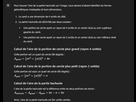
[MATHS] Trouver l'aire de la partie hachurée

Un quart de cercle de rayon 4, un demi-cercle de rayon 2.

[11:18:27] <Zaibre>
A quoi ça m'avance ?

À rien pourquoi.

Le 15 juin 2024 à 11:19:38 MarreDetreSeul a écrit :
Pourquoi t'as fait autant de traits pour un demi cercle

Il a pas le kompa dans l'oeil.

[11:22:00] <jkifsedkjfzlfza>
tu trouves le point où les cercles se croisent puis tu fais deux intégrales

C'est-à-dire.

[11:22:57] <ConteDeFee>
Pourquoi as-tu dessiné le colisée ?

Pas moi le dessin

Le 15 juin 2024 à 11:22:40 :

[11:22:00] <jkifsedkjfzlfza>
tu trouves le point où les cercles se croisent puis tu fais deux intégrales

C'est-à-dire.

Tu trouves les équations des 2 cercles, tu les poses en équation pour trouver le point d'intersection
Tu soustrait l'intégrale de l'un à l'autre sur l'intervalle du point d'intersection vers le droite puis t'ajoute l'intégrale de l'aire du bout tt à gauche

Le 15 juin 2024 à 11:15:08 Stalhblume a écrit :

Un quart de cercle de rayon 4, un demi-cercle de rayon 2.

https://www.youtube.com/watch?v=gPBJgDQdZU0

[11:29:05] <Pangolintoxique>

Le 15 juin 2024 à 11:22:40 :

[11:22:00] <jkifsedkjfzlfza>
tu trouves le point où les cercles se croisent puis tu fais deux intégrales

C'est-à-dire.

Tu trouves les équations des 2 cercles, tu les poses en équation pour trouver le point d'intersection
Tu soustrait l'intégrale de l'un à l'autre puis t'ajoute l'intégrale de l'aire du bout tt à gauche

Mais il y aura des intégrables doubles nan ? Comme l'équation d'un cercle est défini par deux variables...

Le 15 juin 2024 à 11:29:05 :

Le 15 juin 2024 à 11:22:40 :

[11:22:00] <jkifsedkjfzlfza>
tu trouves le point où les cercles se croisent puis tu fais deux intégrales

C'est-à-dire.

Tu trouves les équations des 2 cercles, tu les poses en équation pour trouver le point d'intersection
Tu soustrait l'intégrale de l'un à l'autre puis t'ajoute l'intégrale de l'aire du bout tt à gauche

Ca c'est chiant a faire ca.
T'as 1/4 de grand cercle de rayon 2.
Un demin cercle de rayon 1.

Tu appliques pr*r²

Tu soustrait au grad le petit/

Bien joué, tu es meilleur qu'un terminale lambda.

[11:30:57] <PolloDG2>

Le 15 juin 2024 à 11:29:05 :

Le 15 juin 2024 à 11:22:40 :

[11:22:00] <jkifsedkjfzlfza>
tu trouves le point où les cercles se croisent puis tu fais deux intégrales

C'est-à-dire.

Tu trouves les équations des 2 cercles, tu les poses en équation pour trouver le point d'intersection
Tu soustrait l'intégrale de l'un à l'autre puis t'ajoute l'intégrale de l'aire du bout tt à gauche

Ca c'est chiant a faire ca.
T'as 1/4 de grand cercle de rayon 2.
Un demin cercle de rayon 1.

Tu appliques pr*r²

Tu soustrait au grad le petit/

Bien joué, tu es meilleur qu'un terminale lambda.

J'vois pas comment ça donne l'aire en faisant ça.