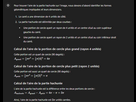
[MATHS] Trouver l'aire de la partie hachurée

Le 15 juin 2024 à 11:32:22 Stalhblume a écrit :

[11:30:57] <PolloDG2>

Le 15 juin 2024 à 11:29:05 :

Le 15 juin 2024 à 11:22:40 :

[11:22:00] <jkifsedkjfzlfza>
tu trouves le point où les cercles se croisent puis tu fais deux intégrales

C'est-à-dire.

Tu trouves les équations des 2 cercles, tu les poses en équation pour trouver le point d'intersection
Tu soustrait l'intégrale de l'un à l'autre puis t'ajoute l'intégrale de l'aire du bout tt à gauche

Ca c'est chiant a faire ca.
T'as 1/4 de grand cercle de rayon 2.
Un demin cercle de rayon 1.

Tu appliques pr*r²

Tu soustrait au grad le petit/

Bien joué, tu es meilleur qu'un terminale lambda.

J'vois pas comment ça donne l'aire en faisant ça.

Ton qi ?

[11:32:48] <Celestinoux>

Le 15 juin 2024 à 11:32:22 Stalhblume a écrit :

[11:30:57] <PolloDG2>

Le 15 juin 2024 à 11:29:05 :

Le 15 juin 2024 à 11:22:40 :

> [11:22:00] <jkifsedkjfzlfza>

> tu trouves le point où les cercles se croisent puis tu fais deux intégrales

C'est-à-dire.

Tu trouves les équations des 2 cercles, tu les poses en équation pour trouver le point d'intersection
Tu soustrait l'intégrale de l'un à l'autre puis t'ajoute l'intégrale de l'aire du bout tt à gauche

Ca c'est chiant a faire ca.
T'as 1/4 de grand cercle de rayon 2.
Un demin cercle de rayon 1.

Tu appliques pr*r²

Tu soustrait au grad le petit/

Bien joué, tu es meilleur qu'un terminale lambda.

J'vois pas comment ça donne l'aire en faisant ça.

Ton qi ?

Environ 80.

Le 15 juin 2024 à 11:32:22 :

[11:30:57] <PolloDG2>

Le 15 juin 2024 à 11:29:05 :

Le 15 juin 2024 à 11:22:40 :

[11:22:00] <jkifsedkjfzlfza>
tu trouves le point où les cercles se croisent puis tu fais deux intégrales

C'est-à-dire.

Tu trouves les équations des 2 cercles, tu les poses en équation pour trouver le point d'intersection
Tu soustrait l'intégrale de l'un à l'autre puis t'ajoute l'intégrale de l'aire du bout tt à gauche

Ca c'est chiant a faire ca.
T'as 1/4 de grand cercle de rayon 2.
Un demin cercle de rayon 1.

Tu appliques pr*r²

Tu soustrait au grad le petit/

Bien joué, tu es meilleur qu'un terminale lambda.

J'vois pas comment ça donne l'aire en faisant ça.

N'importe quoi , les deux bouts de cercles ne sont pas superposés.

[11:34:31] <Rapasteque>

Le 15 juin 2024 à 11:32:22 :

[11:30:57] <PolloDG2>

Le 15 juin 2024 à 11:29:05 :

Le 15 juin 2024 à 11:22:40 :

>[11:22:00] <jkifsedkjfzlfza>

>tu trouves le point où les cercles se croisent puis tu fais deux intégrales

C'est-à-dire.

Tu trouves les équations des 2 cercles, tu les poses en équation pour trouver le point d'intersection
Tu soustrait l'intégrale de l'un à l'autre puis t'ajoute l'intégrale de l'aire du bout tt à gauche

Ca c'est chiant a faire ca.
T'as 1/4 de grand cercle de rayon 2.
Un demin cercle de rayon 1.

Tu appliques pr*r²

Tu soustrait au grad le petit/

Bien joué, tu es meilleur qu'un terminale lambda.

J'vois pas comment ça donne l'aire en faisant ça.

N'importe quoi , les deux bouts de cercles ne sont pas superposés.

Ça me semblait bizarre.

[11:36:46] <Taku[Shiny]>

Malheureusement ChatGPT est très mauvais en maths.

Le 15 juin 2024 à 11:37:03 :
Tout le monde a l'air de trouver ça simple sans trouver en tout cas.

Je t'ai répondu, t'es débile ou quoi ?

[11:37:57] <aAardvark>
Grosse flemme mais j'imagine qu'en donnant l'équation des 2 cercles, en prenant la différence, et en intégrant à partir de la bonne abscisse, ça se fait ?

Je me suis dit la même chose mais il n'y a pas plus simple ?

Le 15 juin 2024 à 11:33:31 :

[11:32:48] <Celestinoux>

Le 15 juin 2024 à 11:32:22 Stalhblume a écrit :

[11:30:57] <PolloDG2>

Le 15 juin 2024 à 11:29:05 :

> Le 15 juin 2024 à 11:22:40 :

> > [11:22:00] <jkifsedkjfzlfza>

> > tu trouves le point où les cercles se croisent puis tu fais deux intégrales

>

> C'est-à-dire.

Tu trouves les équations des 2 cercles, tu les poses en équation pour trouver le point d'intersection
Tu soustrait l'intégrale de l'un à l'autre puis t'ajoute l'intégrale de l'aire du bout tt à gauche

Ca c'est chiant a faire ca.
T'as 1/4 de grand cercle de rayon 2.
Un demin cercle de rayon 1.

Tu appliques pr*r²

Tu soustrait au grad le petit/

Bien joué, tu es meilleur qu'un terminale lambda.

J'vois pas comment ça donne l'aire en faisant ça.

Ton qi ?

Environ 80.

Nan la c'est trop.

Concentre toi d'abord sur ce que ton prof de math te demande. Tu dois etre tres jeune. Petit a petit sans que tu t'en rendes compte, ton cerveau va murir ,grandir et tu pourras résoudres ces problèmes naturellement.

[11:38:25] <Pangolintoxique>

Le 15 juin 2024 à 11:37:03 :
Tout le monde a l'air de trouver ça simple sans trouver en tout cas.

Je t'ai répondu, t'es débile ou quoi ?

Je t'ai répondu khey, sans réponse.

[11:41:20] <The_Professor2>
C'est pour ça que j'ai acheté un garage a louer, j'échappe a toutes ces règles ridicules, je fous a la porte en toute légalité mon locatix s'il paye pas, et il risque pas de dégrader quoi que ce soit

Certes.

Le 15 juin 2024 à 11:37:26 :

[11:36:46] <Taku[Shiny]>

Malheureusement ChatGPT est très mauvais en maths.

c'est si mauvais que ça?