L'hypothèse de Riemann rend ZINZIN

Pourquoi quelque chose qui semble si naturel donne cette impression de n'avoir aucune prise possible ?

Il y a une vidéo intéressante qui montre l'orbite de la fonction eta (elle a les mêmes zéros que zêta et ne diffère d'elle que d'un facteur élémentaire) : https://www.youtube.com/watch?v=wp4_bryCutU

Regardez, il y a comme une force mystérieuse qui interdit l'orbite de traverser l'origine pour autant que sigma>0.5.

https://www.youtube.com/watch?v=9IdkvifRFgU&t=55s une vidéo avec trois orbites, regardez bien la courbe rouge (sigma=0.5) qui est la seule à traverser l'origine.

Donc selon le graph de l'orbite, il doit exister un cercle part le quel l'orbite ne passe jamais et dont le rayon se réduit à mesure que l'on avance vers sigma=1/2. Un tel rayon R(sigma) vérifierait alors Lim sigma->1/2 (R(Sigma))=0. Mais là où ça se complique, c'est de comprendre quelle force mystérieuse est à l'oeuvre derrière la préservation de ce trou.

L'expression utilisée pour le graph de l'orbite (pour k=infini) :
Partie réelle :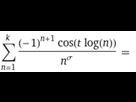
Partie imaginaire :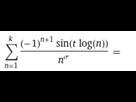

Même si ces deux expressions ne semblent n'avoir rien en commun avec les nombres premiers et être purement analytiques, l'identité log(a*b)=log(a)+log(b) montre comment les nombres premiers interviennent dans le cos/sin. Le problème c'est que les deux séries données ne convergent que conditionnellement sauf erreur. C'est aussi souvent ça qui rend RH si difficile, il fait intervenir des objets très sensibles dont la modification entrainent souvent la perte des propriétés intéressantes. Ce qui, je pense, suggère qu'il y a un fait possiblement fondamental derrière le problème, quelque chose qui ressemblerait à une restriction. Peut-être une loi qui régit le lien entre propriété multiplicative et additive, un lien codé par la fonction zêta via le produit Eulérien Ca montre en tout cas que la fonction zêta est un objet très spécial

Mais on a tellement aucun indice sur ce qu'il se passe, juste certaines analogies qui pourraient faire penser à un lien avec par exemple, la théorie des opérateurs, mais c'est bien loin d'être suffisant.

Sérieusement ce problème rend zinzin et ce qui est vraiment déprimant c'est cette impression qu'on a juste pas les outils nécessaires pour prouver quoique ce soit de vraiment fort, par exemple, une région sans zéro. Mais même ça, ça n'a pas beaucoup évolué en 160 ans (la grande avancée fut le théorème des nombres premiers).

Des kheys matheux pour en discuter ?

Le 10 juillet 2022 à 13:43:46 :
tu connais le théorème de Voronin sur zéta ?

Sur l'universalité ? Oui, il me semble qu'on sait désormais que l'universalité est une propriété extrêmement fréquente pour les fonctions analytiques, ça n'en reste pas moins fascinant

Le 10 juillet 2022 à 13:45:49 :
C'est quoi une orbite?

C'est l'image de la fonction êta sur le plan complexe. En abscisse tu as la partie réelle et en ordonnée la partie imaginaire. Regarde la vidéo, tu vois l'orbite se tracer pour t de plus en plus grand.

Pourquoi quelque chose qui semble si naturel

Ah bon

Le 10 juillet 2022 à 13:47:08 :
Dieu, voila la réponse

Dur de se satisfaire de ce type de réponse

Le 10 juillet 2022 à 13:47:59 :

Pourquoi quelque chose qui semble si naturel

Ah bon

Oui. Un bon exemple du côté "naturel" du problème :

Considère la fonction de moebius, elle prend la valeur 1 lorsque n est le produit d'un nombre pair de nombres premiers distincts, -1 lorsque n est le produit d'un nombre impair de nombres premiers distincts et 0 sinon.

Considère maintenant la fonction sommatoire de la fonction de Moebius, que l'on notera M(x) (tu sommes sur les n<=x). L'hypothèse de Riemann prédit alors que M(x)=O(x^(0.5+epsilon)), pour tout epsilon>0. C'est ce à quoi on s'attendrait en numérotant chaque face d'une pièce et en sommant chaque résultat obtenu en la lançant. Donc en ce sens, la distribution que prédit l'hypothèse de Riemann est tout ce qu'il y a de plus naturelle.

Le 10 juillet 2022 à 13:46:51 :

Le 10 juillet 2022 à 13:45:49 :
C'est quoi une orbite?

C'est l'image de la fonction êta sur le plan complexe. En abscisse tu as la partie réelle et en ordonnée la partie imaginaire. Regarde la vidéo, tu vois l'orbite se tracer pour t de plus en plus grand.

Ton topic est intéressant, mais tu ne poses pas assez les définitions, ni les fonctions.
On ne comprend pas très bien quoi est quoi, c'est dommage

Le 10 juillet 2022 à 13:51:52 :
T'es à quel niveau scolaire ?

desco

Le 10 juillet 2022 à 13:52:30 :

Le 10 juillet 2022 à 13:46:51 :

Le 10 juillet 2022 à 13:45:49 :
C'est quoi une orbite?

C'est l'image de la fonction êta sur le plan complexe. En abscisse tu as la partie réelle et en ordonnée la partie imaginaire. Regarde la vidéo, tu vois l'orbite se tracer pour t de plus en plus grand.

Ton topic est intéressant, mais tu ne poses pas assez les définitions, ni les fonctions.
On ne comprend pas très bien quoi est quoi, c'est dommage

Oui pardon khey j'ai un peu parler comme si on était sur un forum dédié à ce problème

Le 10 juillet 2022 à 13:53:25 :
y'a le khey sinus qui parlait d'un rapprochement avoir la conjecture d'Hilbert-Polya

Je pense que plusieurs opérateurs ont été proposés, notamment par Alain Connes

Le 10 juillet 2022 à 13:56:16 :
Je suis en école d'ingénieur (CS) et je comprends rien kheyou

Connais-tu un peu l'hypothèse de Riemann/fonction zêta ou pas du tout ?

J'ai donné un exemple d'un équivalent assez simple à comprendre :

Le 10 juillet 2022 à 13:52:22 :

Le 10 juillet 2022 à 13:47:59 :

Pourquoi quelque chose qui semble si naturel

Ah bon

Oui. Un bon exemple du côté "naturel" du problème :

Considère la fonction de moebius, elle prend la valeur 1 lorsque n est le produit d'un nombre pair de nombres premiers distincts, -1 lorsque n est le produit d'un nombre impair de nombres premiers distincts et 0 sinon.

Considère maintenant la fonction sommatoire de la fonction de Moebius, que l'on notera M(x) (tu sommes sur les n<=x). L'hypothèse de Riemann prédit alors que M(x)=O(x^(0.5+epsilon)), pour tout epsilon>0. C'est ce à quoi on s'attendrait en numérotant chaque face d'une pièce et en sommant chaque résultat obtenu en la lançant. Donc en ce sens, la distribution que prédit l'hypothèse de Riemann est tout ce qu'il y a de plus naturelle.