[MATHS] Les khey MATHEMATICIENS

Le théorème de la boule chevelue

https://fr.m.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_la_boule_chevelue

C'est pas forcément hyper difficile mais historiquement ça a longtemps été admis sans démonstration car on savait pas le démontrer rigoureusement

Théorème de Jordan

Théorème des valeurs intermédiaires

Démontrer que tout nombre rationnel est la somme des cubes de trois nombres rationnels.

Solution :

Le 21 avril 2022 à 15:34:54 :
C'est pas forcément hyper difficile mais historiquement ça a longtemps été admis sans démonstration car on savait pas le démontrer rigoureusement

Théorème de Jordan

Théorème des valeurs intermédiaires

Le TVI se démontre à partir du théorème de Rolle?

Considérons deux carrés de coté 2 ayant le meme centre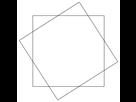

Expliquer pourquoi l'aire de leur intersection est plus grande que 3

Solution :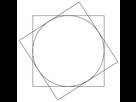Puisque ils ont le meme centre, ils ont en particulier le meme cercle inscrit
L'aire de leur intersection est alors évidemment supérieure à l'aire de ce cercle
Cercle dont l'aire vaut π > 3
CQFD

Le 21 avril 2022 à 15:42:00 :
On demande un théorème intuitif ca parle de topologie, d'Euler, d'intégrale. Changez rien les prépa

Le fait que la méthode d'Euler pour résoudre des EDO soit convergente à l'ordre 1 c'est intuitif khey

Si, à l'aide d'un crayon, on dessine une ligne continue (on ne lève pas le crayon) qui ne se croise pas et qui termine là où elle commence, la zone de la feuille non dessinée se décompose en deux parties, l'intérieur de la figure, qui est borné, et l'extérieur, qui ne le serait pas si la feuille ne l'était pas

La preuve est tres tres dure

Le 21 avril 2022 à 15:39:26 :

Le 21 avril 2022 à 15:34:54 :
C'est pas forcément hyper difficile mais historiquement ça a longtemps été admis sans démonstration car on savait pas le démontrer rigoureusement

Théorème de Jordan

Théorème des valeurs intermédiaires

Le TVI se démontre à partir du théorème de Rolle?

Non, déjà le théorème de Rolle demande plus de régularité à la fonction que le TVI (dérivabilité contre continuité). Le théorème des valeurs intermédiaires est une conséquence du principe de borne supérieure. En fait, le TVI provient du fait que les connexes de R sont les intervalles, et on démontre ça grâce à la propriété de la borne supérieure (tout ensemble non-vide et majoré dans R possède une borne supérieure dans R).

Le théorème de Rolle par contre, est une conséquence du théorème des bornes (qui lui repose sur le théorème de Borel-Lebesgue : les compacts de R sont les ensembles fermés bornés; théorème qui repose lui aussi sur la propriété de la borne supérieure).

Sinon pour moi, le théorème intuitif mais difficile à démontrer, c'est bien le théorème de Jordan

Théorème de Jordan

Mais dans l'autre sens, un des théorème les moins intuitif : Théorème de Borsuk-Ulam