[MATHS] question pour l'élite

[20:09:50] <celestinent>

Le 13 septembre 2021 à 19:59:40 :
Minimum en x = -3

non plus

Bah si le desco
El famosso 17 de moyenne
J'espère que c'est faux, sinon le niveau de la France est vraiment nul à chier

Le 13 septembre 2021 à 20:12:03 Farine2Ble a écrit :

[20:09:50] <celestinent>

Le 13 septembre 2021 à 19:59:40 :
Minimum en x = -3

non plus

Bah si le desco
El famosso 17 de moyenne
J'espère que c'est faux, sinon le niveau de la France est vraiment nul à chier

En même temps, on demande le minimum pas le x

Le 13 septembre 2021 à 20:16:02 Bedivere112 a écrit :
Il doit être en bac pro pour avoir 17 de moyenne sans savoir faire ça
Bref...
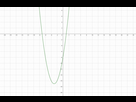
f(x)=x²+6x-8
f'x) = 2x + 6
f'(x) = 0 <=> x = - 3
A toi de determiner si c'est un min ou un max en faisant la dérivée seconde

Pas besoin de la dérivée seconde

Le 13 septembre 2021 à 20:09:37 celestinent a écrit :

Le 13 septembre 2021 à 20:06:26 :
On révise l'op
https://www.methodemaths.fr/polynome_second_degre/

merci

De rien

Je sais pas si tu as fais ça en classe, mais sinon tu fait une étude de dérivée

f(x) = x² + 6x - 8
f'(x) = 2x + 6

On cherche à savoir pour quelle valeur de x, la dérivée s'annule (= maximum ou minimum de f(x))

2x + 6 = 0
x = -6 / 2 = -3

On remplace dans f(x) :
f(-3) = (-3)²+6(-3) - 8 = 9 - 18 - 8 = -17

Le 13 septembre 2021 à 20:16:02 :
Il doit être en bac pro pour avoir 17 de moyenne sans savoir faire ça
Bref...
f(x)=x²+6x-8
f'x) = 2x + 6
f'(x) = 0 <=> x = - 3

La derivee seconde d'un polynome du second degre

Le 13 septembre 2021 à 20:17:04 tokpela a écrit :

Le 13 septembre 2021 à 20:09:37 celestinent a écrit :

Le 13 septembre 2021 à 20:06:26 :
On révise l'op
https://www.methodemaths.fr/polynome_second_degre/

merci

De rien

Je sais pas si tu as fais ça en classe, mais sinon tu fait une étude de dérivée

f(x) = x² + 6x - 8
f'(x) = 2x + 6

On cherche à savoir pour quelle valeur de x, la dérivée s'annule (= maximum ou minimum de f(x))

2x + 6 = 0
x = -6 / 2 = -3

On remplace dans f(x) :
f(-3) = (-3)²+6(-3) - 8 = 9 - 18 - 8 = -17

Il faut également ajouté que le coefficient a > 0 donc il s'agit d'un minimum.

Etant une parabole :

La courbe est décroissante jusqu'en f(-3)=-17 puis croissante

Le 13 septembre 2021 à 20:17:21 :

Le 13 septembre 2021 à 20:16:02 :
Il doit être en bac pro pour avoir 17 de moyenne sans savoir faire ça
Bref...
f(x)=x²+6x-8
f'x) = 2x + 6
f'(x) = 0 <=> x = - 3

La derivee seconde d'un polynome du second degre

Désolé Celestin j'ai terminé le lycée depuis des années, je me souviens pas de de l'intégralité de tes cours de segpa

Le 13 septembre 2021 à 20:22:28 :
tiens l'op

merci mais c'est surtout la 1, je suis confus

Le 13 septembre 2021 à 20:21:38 celestinent a écrit :
merci pour votre aide
mais c'est -3 ou -17 la réponse? On n'a jamais parlé de dérivée nous...

Je suppose qu'on t'a plutôt donné le -b/2a ?

En faisant ça on trouve le maximum/minimum en x.

f(-b/2a) = -17 (la réponse) est l'extremum de ton polynôme (hors infini)

C'est un minimum car a>0

Le 13 septembre 2021 à 20:23:35 :

Le 13 septembre 2021 à 20:22:28 :
tiens l'op

merci mais c'est surtout la 1, je suis confus

comment ça la 1?

Le 13 septembre 2021 à 20:19:10 Ass2Trefle a écrit :

Le 13 septembre 2021 à 20:17:04 tokpela a écrit :

Le 13 septembre 2021 à 20:09:37 celestinent a écrit :

Le 13 septembre 2021 à 20:06:26 :
On révise l'op
https://www.methodemaths.fr/polynome_second_degre/

merci

De rien

Je sais pas si tu as fais ça en classe, mais sinon tu fait une étude de dérivée

f(x) = x² + 6x - 8
f'(x) = 2x + 6

On cherche à savoir pour quelle valeur de x, la dérivée s'annule (= maximum ou minimum de f(x))

2x + 6 = 0
x = -6 / 2 = -3

On remplace dans f(x) :
f(-3) = (-3)²+6(-3) - 8 = 9 - 18 - 8 = -17

Il faut également ajouté que le coefficient a > 0 donc il s'agit d'un minimum.

Etant une parabole :

La courbe est décroissante jusqu'en f(-3)=-17 puis croissante

Bien vu, le signe de a est à prendre en compte

Ceci dit l'exercice demande un minimum, donc je sais pas si il faut justifier que c'est bien un minimum

On définit la fonction f sur R par f(x)=x²+6x-8

donc f'(x)=2x+6

le coefficient est positif, la fonction f possède donc un minimum

or, le minimum d'une fonction est atteint quand sa dérivée est égale à 0

on pose f'(x)=0

2x+6=0
2x=-6
x=-3

f(-3)=9-18-8=-17

donc le minimum de la fonction se situe en (-3,-17)

Le 13 septembre 2021 à 20:25:58 Arceus19974 a écrit :
C'est égal à (x + 3)² - 17, le minimum est donc -17 atteint en -3.

On peut factoriser effectivement

Le 13 septembre 2021 à 20:25:35 :

Le 13 septembre 2021 à 20:23:35 :

Le 13 septembre 2021 à 20:22:28 :
tiens l'op

merci mais c'est surtout la 1, je suis confus

comment ça la 1?

question 1