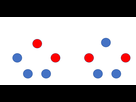
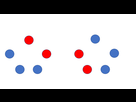
[Math] venez compter des sapins avec moi svp ...

question : Un truc tout bête : n sapins, m d'une variété et (m-n) d'une autre...

on les range en cercle.

Combien d'arrangements possibles ?

réponse :

J'ai tendance à dire, je fixe un sapin et j'arrange les autres autour de lui... ce qui me donne, si je fixe un sapin de la première catégorie :

(n-1)! / m! (m-n-1)!

ou alors, si je fixe un sapin de la seconde catégorie :

(n-1)!/(m-1)!(m-n-1)!

... je dois additionner ces deux nombres ? Je suis toujours tout perdu avec ces trucs ... j'aurais tendance à additionner et dire :

(n-1)! / m! (m-n-1)! + (n-1)!/(m-1)!(m-n-1)!

arrangements possibles, en cercle de ces n sapins. Quelqu'un pour me confirmer ? Pour moi ça a du sens mais... peut-être que je me plante complet.

Compte le nombre de combinaisons possibles avec les deux types d'arbres
Puis le nombre de permutations possibles

Le nombre d'arrangements c'est combi*permut

Le 30 mars 2021 à 18:59:10 TintinEnOr a écrit :
Compte le nombre de combinaisons possibles avec les deux types d'arbres
Puis le nombre de permutations possibles

Le nombre d'arrangements c'est combi*permut

j'ai oublié de préciser qu'on ne discerne pas les arbres d'une même catégorie entre eux !

C'est le cercle hein qui rend la chose un peu plus vicieuse.

(n-1)! / m! (m-n-1)! + (n-1)!/(m-1)!(m-n-1)!

ce nombre fait sens pour moi .... Mais j'suis absolument pas sûr de moi. Si y a quelqu'un pour me dire que c'est complètement faux ou complètement juste :

Mal écrit du coup ça n'a pas de sens ... je voulais dire :

(n-1)! / m! (n-m-1)! + (n-1)!/(m-1)!(n-m)! ...

compter ce genre de trucs quoi... ici avec n=5 et m=3 .

Du coup ma formule me renvoie 10 possibilités ... ça semble correct. J'vais garder ça si personne me contredit...

Le 30 mars 2021 à 19:17:37 Sobamask a écrit :
Sacrés arabes

Tu veux les compter à rotation/permutation circulaire près ?
La formule va dépendre du pgcd de n et m dans ce cas. Il y a des motifs de plus au moins grandes périodes.

Si m et n sont premiers entre eux ce sera juste 1/n * (m parmi n)

(n-1)! / m! (n-m-1)! + (n-1)!/(m-1)!(n-m)! = [ (n-1)! (n-m) + (n-1)! m ]/(m)!(n-m)! = (n-1)! n / (m)!(n-m)! = n! /(m)!(n-m)!

et je compte sur une p****n de ligne........

bordel je suis trop nul avec ces dénombrements... du coup pas moyen de voir le cercle ici.

Le 30 mars 2021 à 19:37:02 Motocultage a écrit :
Tu veux les compter à rotation/permutation circulaire près ?
La formule va dépendre du pgcd de n et m dans ce cas. Il y a des motifs de plus au moins grandes périodes.

Si m et n sont premiers entre eux ce sera juste 1/n * (m parmi n)

Oui, comme tu dis : à une rotation près.

ces deux ci comptent pour 1 p.ex

Je vois que les kheys n'ont pas plus que moi l'habitude de compter les sapins

C'est quand même bête... si on a n boules numérotées de 1 à n (toutes discernables donc) on peut juste dire (n-1)! et ma logique marchait. Sauf que dès qu'on joue avec des boules de deux couleurs, deux catégories ... j'y arrive plus. Bon, si je trouve je communiquerai la réponse ici.

Le 30 mars 2021 à 19:59:31 PrepaMaths a écrit :
Je pense meme que y a une histoire dindicatrice d'euler...

ah oui quand même

déjà vu ça en théorie des nombres... cardinal de l'ensemble des diviseurs premiers ? un truc du genre... .

Attends, comme disait un vdd :

... ce sera juste 1/n * (m parmi n)

pourquoi on ne peut pas se contenter de ceci ?

Si m et n sont premiers entre eux ...

En quoi ça nous embête ici le fait que les nombres puissent ne pas être premiers entre eux ? Je crois que je visualise mal la problématique...