Y a un t-il un surdoué en c++ ici?

2 posts, et le mec a toujours pas mis son foutu exo.

Ton QI l'OP ?

Le 10 mai 2024 à 13:52:28 Dreamer_afrik a écrit :

C'est quoi l'exo ?

Le 10 mai 2024 à 13:54:35 :
Trouver la somme des 200 premiers termes de de cette suite coder sur C++

Tu demandes un surdoué en C++ pour un truc faisable par un type qui a découvert le language y'a 1 heure

Le 10 mai 2024 à 13:54:35 Dreamer_afrik a écrit :
Trouver la somme des 200 premiers termes de de cette suite coder sur C++

C'est de l'algo, go chatgpt

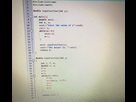
long double f_exp(long double x) {
  long double s = 0., p = 1., f = 1.;
  for (int i = 1; i < 201; i++) {
    s += p/f;
    p *= x;
    f *= i;
  }
  return s;
}

utilise des long double pour la précision, et calcule pas la puissance / factorielle à chaque itération tu peux cumuler

Sur l'image que vous avez partagée, nous voyons la série de Maclaurin pour la fonction exponentielle, \( e^x \). La série est exprimée comme suit :

\[
e^x = \sum_{n=0}^{\infty} \frac{x^n}{n!}
\]

Pour calculer la somme des 200 premiers termes de cette série lorsque \( x \) est donné, nous pouvons utiliser le langage de programmation C++ pour effectuer ce calcul. Voici un exemple de code C++ qui réalise cette opération :

```cpp

1. include <iostream>
2. include <cmath> // Pour utiliser pow() et factorial

// Fonction pour calculer le factoriel
double factorial(int n) {
double fact = 1;
for (int i = 1; i <= n; ++i) {
fact *= i;
}
return fact;
}

int main() {
double x;
std::cout << "Entrez la valeur de x pour laquelle vous voulez calculer e^x: ";
std::cin >> x;

double sum = 0;
int terms = 200; // Nombre de termes à calculer

for (int n = 0; n < terms; ++n) {
sum += pow(x, n) / factorial(n);
}

std::cout << "La somme des 200 premiers termes de la série de Maclaurin pour e^x est: " << sum << std::endl;

return 0;
}
```

Ce code demande à l'utilisateur d'entrer une valeur pour \( x \), puis calcule la somme des 200 premiers termes de la série de Maclaurin pour \( e^x \) en utilisant une boucle for pour additionner chaque terme jusqu'à 199. Le résultat est ensuite affiché. Vous pouvez compiler et exécuter ce code dans un environnement C++ standard.