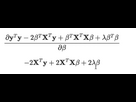Topic de
584189489289982
:
[MATHS] Dériver par rapport à un vecteur
Supprimé- 1
Je comprend pas, pour moi derivé selon une variable réel x = lim h - > 0 (f(a+h)-f(a))/h Donc quelle est cette sorcellerie 
Le 29 février 2024 à 02:02:09 :
Je comprend pas, pour moi derivé selon une variable réel x = lim h - > 0 (f(a+h)-f(a))/h Donc quelle est cette sorcellerie
Tu derives par rapport a Beta donc le resultat est trivial 
Le 29 février 2024 à 02:03:31 :
Le 29 février 2024 à 02:02:09 :
Je comprend pas, pour moi derivé selon une variable réel x = lim h - > 0 (f(a+h)-f(a))/h Donc quelle est cette sorcellerieTu derives par rapport a Beta donc le resultat est trivial
Ca ne m'aide pas vraiment 
Visiblement le résultat est identique à ce qu'on obtiendrai si on considère beta comme un réel mais je comprend pas ce que ca signifie
- 1
Données du topic
- Auteur
- 584189489289982
- Date de création
- 29 février 2024 à 02:02:09
- Date de suppression
- 15 mars 2024 à 07:54:00
- Supprimé par
- Auteur
- Nb. messages archivés
- 5
- Nb. messages JVC
- 5
En ligne sur JvArchive 98