Besoin d’un crack en MATH
- 1
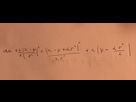
Gauche l’equation dont on part puis a droite le résultat attendu ( c’est la correction)
Sauf que le soucis ,je ne sais pas comment ils ont fait pour trouver le terme à droite, si un khey fort en math peut me détailler tout le calcul ce serais top
Le 22 octobre 2023 à 17:38:41 :
Chat gpt👍
Le 22 octobre 2023 à 17:38:41 :
Chat gpt👍
Chat gpt pas ouf il fait beaucoup d’erreur
Le 22 octobre 2023 à 17:40:49 :
Développe tout
C’est ce que j’ai fais mais je galère à retrouver le résultat
Le 22 octobre 2023 à 17:41:11 :
Je regarde ça
Merci beaucoup khey
ax+(x-u)²/(2s²) = (x-u+as²)²/(2s²)+a(u-as²/2) ?
ax+(x-u)²/(2s²)= [2s²ax+(x-u)² ] /(2s²)
= [(x-u)²+(as²)²+2(x-u)as²-(as²)²-2(x-u)as²+2s²ax ] /(2s²)
=[(x-u+as)²-(as²)²-2(x-u)as²+2s²ax]/(2s²)
=(x-u+as)²/(2s²) - (as)²/2-a(x-u)+ax
=(x-u+as)²/(2s²) - (as)²/2+au
=(x-u+as)²/(2s²) + a(u-as²/2)
Ca c'est si tu veux obtenir la forme de droite en t'autorisant uniquement à modifier celle de gauche.
Mais sinon le plus simple est tout simplement de développer ce qui est à gauche, ce qui est à droite, et de constater que c'est identique.
mais moi c'est pas des maths
Ce qui donne :
A= ax+(x-u)²/(2s²)
A= ax +x²/(2s²) +u²/(2s²)-2ux/(2s²)
A=ax +x²/(2s²) +u²/(2s²)-ux/s²
B=(x-u+as²)²/(2s²)+a(u-as²/2)
B= x²/(2s²)+u²/(2s²)+a²s^4/(2s²)-2ux/(2s²)-2aus²/(2s²)+2xas²/(2s²)+au-a²s²/2
B= x²/(2s²)+u²/(2s²)+a²s²/2-ux/s²-au+xa+au-a²s²/2
B= x²/(2s²)+u²/(2s²)-ux/s²+xa
B= ax +x²/(2s²)+u²/(2s²)-ux/s²
B=A
Le 22 octobre 2023 à 17:56:17 :
Ce qui donne :A= ax+(x-u)²/(2s²)
A= ax +x²/(2s²) +u²/(2s²)-2ux/(2s²)
A=ax +x²/(2s²) +u²/(2s²)-ux/s²B=(x-u+as²)²/(2s²)+a(u-as²/2)
B= x²/(2s²)+u²/(2s²)+a²s^4/(2s²)-2ux/(2s²)-2aus²/(2s²)+2xas²/(2s²)+au-a²s²/2
B= x²/(2s²)+u²/(2s²)+a²s²/2-ux/s²-au+xa+au-a²s²/2
B= x²/(2s²)+u²/(2s²)-ux/s²+xa
B= ax +x²/(2s²)+u²/(2s²)-ux/s²
B=A
Merci bcp khey je vais mettre ça sur ma feuille et vérifier, si j’ai des questions je te dm t’es quelqu’un de brave 
Le 22 octobre 2023 à 17:51:59 :
ax+(x-u)²/(2s²) = (x-u+as²)²/(2s²)+a(u-as²/2) ?ax+(x-u)²/(2s²)= [2s²ax+(x-u)² ] /(2s²)
= [(x-u)²+(as²)²+2(x-u)as²-(as²)²-2(x-u)as²+2s²ax ] /(2s²)
=[(x-u+as)²-(as²)²-2(x-u)as²+2s²ax]/(2s²)
=(x-u+as)²/(2s²) - (as)²/2-a(x-u)+ax
=(x-u+as)²/(2s²) - (as)²/2+au
=(x-u+as)²/(2s²) + a(u-as²/2)Ca c'est si tu veux obtenir la forme de droite en t'autorisant uniquement à modifier celle de gauche.
Mais sinon le plus simple est tout simplement de développer ce qui est à gauche, ce qui est à droite, et de constater que c'est identique.
Je suis surement con ou c'est mal expliquer mais comment on peut passer de l'expression de [2s²ax+(x-u)² ] /(2s²)
à = [(x-u)²+(as²)²+2(x-u)as²-(as²)²-2(x-u)as²+2s²ax ] /(2s²) ?
- 1
Données du topic
- Auteur
- antivaxnotoire
- Date de création
- 22 octobre 2023 à 15:37:23
- Nb. messages archivés
- 15
- Nb. messages JVC
- 15

