[PHOTO] Le produit scalaire : on peut dire que c'est la distance ?

Le produit scalaire : on peut dire que c'est la distance d'un point à un autre ?

Le 22 mars 2023 à 18:32:26 :
Tu fais un print

quoi ?

Le 22 mars 2023 à 18:31:15 :
Le produit scalaire : on peut dire que c'est la distance d'un point à un autre ?

non pas du tout

Le 22 mars 2023 à 18:33:00 :

Le 22 mars 2023 à 18:31:15 :
Le produit scalaire : on peut dire que c'est la distance d'un point à un autre ?

non pas du tout

MB c'est la norme dcp qui est la longueur d'un vecteur mais le produit scalaire géométriquement parlant c'est quoi ?

Le 22 mars 2023 à 18:33:00 :

Le 22 mars 2023 à 18:31:15 :
Le produit scalaire : on peut dire que c'est la distance d'un point à un autre ?

non pas du tout

C'est une forme bilineaire symétrique et définie positive
Elle prend 2 vecteurs de ton EV et lui associe un scalaire
Un produit scalaire peut être défini par une intégrale par exemple..

Le 22 mars 2023 à 18:35:30 :

Le 22 mars 2023 à 18:33:00 :

Le 22 mars 2023 à 18:31:15 :
Le produit scalaire : on peut dire que c'est la distance d'un point à un autre ?

non pas du tout

C'est une forme bilineaire symétrique et définie positive
Elle prend 2 vecteurs de ton EV et lui associe un scalaire
Un produit scalaire peut être défini par une intégrale par exemple..

oui ça je comprends mais pourquoi les coordonnées de x dans la base B sont (<x,e1>,...<x,en>) ?

Le 22 mars 2023 à 18:34:39 :
Non ça veut dire qu'un vecteur est exprimable dans une base comme la somme des produits scalaires du vecteur de chaque vecteur de la abse

Chaque vecteur est exprimable dans une base qui est une base de produits scalaires ?

[18:37:30] <KikogZ>

Le 22 mars 2023 à 18:35:30 :

Le 22 mars 2023 à 18:33:00 :

Le 22 mars 2023 à 18:31:15 :
Le produit scalaire : on peut dire que c'est la distance d'un point à un autre ?

non pas du tout

C'est une forme bilineaire symétrique et définie positive
Elle prend 2 vecteurs de ton EV et lui associe un scalaire
Un produit scalaire peut être défini par une intégrale par exemple..

oui ça je comprends mais pourquoi les coordonnées de x dans la base B sont (<x,e1>,...<x,en>) ?

Prends un exemple simple genre dans R^n, la base formée par les vecteurs avec un 1 à la coordonée i et 0 partout ailleurs.
Alors pour x=(x_1,...,x_n) tu auras <x,e_i>=x_i pour tout i, et les x_ie_i ce sont juste les (0,...,x_i,..0) où x_i est à la position i (décomposition qu'on pourrait deviner sans avoir recours à la propriété)

Dans le cas général, pour décomposer ton vecteur sur une base quelconque tu utilises cette propriété

Tu peux le voir comme une sorte de projection orthogonale d'un vecteur sur l'autre à un facteur norme du vecteur près.

Si A était un vecteur unitaire, alors la distance en vert serait directement le produit scalaire.

Le 22 mars 2023 à 18:40:31 :
Parce que c'est une base orthonormée donc :
si x = x1e1 + ... + xnen
Alors par exemple <x,e1> = <x1e1,e1> + ... + <xnen,e1> = x1

d'accord merci !!

Le 22 mars 2023 à 18:41:09 :
Non, le produit scalaire de deux vecteurs quantifie plutôt l'angle entre ces deux vecteurs (sauf qu'il est aussi proportionnel à chacune de leurs normes).

merci !

Le 22 mars 2023 à 18:46:51 :
Tu peux le voir comme une sorte de projection orthogonale d'un vecteur sur l'autre à un facteur norme du vecteur près.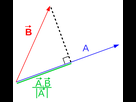

Si A était un vecteur unitaire, alors la distance en vert serait directement le produit scalaire.

Ce que ça veut dire, c'est que si on veut écrire B en fonction de A, alors on aurait B=(A.B)A + C où (A.B) est le produit scalaire de A et B et C est une composante orthogonale à A.
Donc le produit scalaire quantifie la composante de vecteur A qu'il y a dans le vecteur B.