[MATHS][PREPA] Trois mois avant les oraux, êtes-vous ready ?

Après trois ans de travail acharné, te voilà enfin devant la porte des oraux d'admission de la prestigieuse École Polytechnique.

L'examinateur arrive d'un pas nonchalant, un gobelet de café dans une main, l'autre dans la poche.

Sans te regarder, sans même t'adresser un bonjour, il écrit ceci au tableau :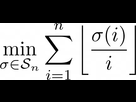

Puis, dans un silence de mort, il s'assoit au fond de la salle et te scrute du regard. "Je vous écoute."

----> ta réac' ?

"Ah o-oui euh une somme et une permutation, il f-faut peut-être penser à la formule du déterminant ? "

"..."

Le 23 février 2023 à 21:21:05 :
Je passe que centrale et mines c’est réglé

Y a des exos de probas à tous les concours khey

Le 23 février 2023 à 21:22:32 :
Je me réveille et pousse un soupir de soulagement en réalisant que ça fait 10 ans que j'ai passé mes oraux

D'accord khey mais l'interprétation cohomologique de la formule d'Ostrogradski est au programme de PT maintenant

Je lui répondrais quelque chose comme ça:

Chaque cycle de la décomposition de sigma en cycles contribue au moins pour 1 à la somme. De plus, un cycle contribue pour 1 ssi de la forme (a_1 a_2 ... a_k) avec a_i<a_{i+1} et a_k<2 a_1.
Dans la classe de conjugaison de sigma, on minimise donc la somme si tous les cycles ne comportent que des entiers consécutifs, et de plus les cycles les plus courts ont les entiers les plus petits.
De plus, il n'est jamais avantageux d'avoir un cycle commençant par a qui contribue d>1, car l'union disjointe de d cycles optimaux donc le premier commence par a serait plus longue.
Une permutation qui minimise la somme sera donc
(1)(23)(4567)...(2^k ... 2^{k+1}-1)...
et le minimum de la somme sera 1+E(log_2(n)).

Le 23 février 2023 à 21:22:24 :

Le 23 février 2023 à 21:21:05 :
Je passe que centrale et mines c’est réglé

Y a des exos de probas à tous les concours khey

C est quoi le rapport aya

Le 24 février 2023 à 00:04:03 :
Je lui répondrais quelque chose comme ça:

Chaque cycle de la décomposition de sigma en cycles contribue au moins pour 1 à la somme. De plus, un cycle contribue pour 1 ssi de la forme (a_1 a_2 ... a_k) avec a_i<a_{i+1} et a_k<2 a_1.
Dans la classe de conjugaison de sigma, on minimise donc la somme si tous les cycles ne comportent que des entiers consécutifs, et de plus les cycles les plus courts ont les entiers les plus petits.
De plus, il n'est jamais avantageux d'avoir un cycle commençant par a qui contribue d>1, car l'union disjointe de d cycles optimaux donc le premier commence par a serait plus longue.
Une permutation qui minimise la somme sera donc
(1)(23)(4567)...(2^k ... 2^{k+1}-1)...
et le minimum de la somme sera 1+E(log_2(n)).

GG mon khey c'est X sans rien branler pour toi