J'explique aux DESCOS le topic-boucle "Cédric Villani te choppe par le col"

Cédric Villani te choppe par le col : "La suite 1/n²(sin(n)) converge t-elle ?"

Qu'est-ce qu'une suite qui converge ?

Une suite est une suite de nombre.

Par exemple la suite 1, 3, 5, 7, etc. Les termes de la suite sont numérotés (le 1er, le 2ème, le 3ème etc). Dans l'exemple, le deuxième terme est 3, le quatrième est 7.

Une suite converge si elle se rapproche toujours plus d'un certain nombre.

Par exemple, la suite "1/n" : Elle converge vers 0. Le premier terme est 1/1 = 1 (on remplace "n" par 1), le deuxième terme est 1/2 = 0,5 (on remplace "n" par 2), le troisième terme est 1/3 = 0,333 (on remplace "n" par 3), etc. On se rapproche toujours un peu plus vers 0, donc la suite converge (vers 0, mais ça pourrait être vers n'importe quel autre nombre).

Que veut dire "sin(n)" ?

"sin" est la fonction "sinus", une fonction bizarre, qui ressemble à ce qu'on voit sur un oscilloscope (un truc qui ressemble à un très vieil ordinateur, qui n'existe que dans les films et dans les salles de TP de lycée) :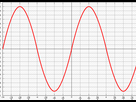

"sin(n)" est donc une suite, le premier terme étant "sin(1)", le deuxième "sin(2)" etc.
Pour trouver sin(1), on regarde le graphique ci-dessus, on cherche le "1" sur l'axe horizontale (on cherche environ pi/3, car pi est presque égal à 3). Au niveau de 1 (ou pi/3), on voit que la courbe est en haut du plan. La valeur de sin(1) est donc une valeur élevée, à peu près égale à 0,8. 0,8 est donc le premier terme de la suite "sin(n)".

La problématique :

La question de Cédric Villani est en apparence simple, puis complexe quand on réfléchie un peu, puis de nouveau simple quand on réfléchie bien.

En apparence, on se dit que "n²(sin(n)" est une suite qui va vers l'infini, et que plus le "n" est grand, plus le n-ième terme de cette suite (qui est n²(sin(n)) sera grand. En effet, la suite "n²" va très vite vers l'infini : le premier terme est 1, le deuxième est 4 (= 2²), le troisième est 9 (= 3²) etc. Par conséquent, "1/n²(sin(n))" est un tout petit nombre (très proche de 0) quand n est grand (car on divise le nombre "1" par un nombre très grand, ça donne un nombre très petit).

Mais le "sin(n)", lui, a un comportement imprévisible : Selon la valeur de n, il vaudra parfois 0,697 ou parfois -0,386 ou n'importe quel autre nombre. Donc n²(sin(n) pourrait être très grand, ou très petit, ou négatif pour un certain "n", et pour le "n" suivant (c'est ç dire n+1) il pourrait être totalement différent. Ainsi, on ne sait pas si "1/n²(sin(n))" se rapproche de 0 ou non, quand n est très grand !

Donc quelle est la réponse ?

La réponse est : Non, cette suite ne converge pas.

La vulgarisation de la démonstration étant assez longue à écrire, retenez simplement qu'on peut trouver facilement une suite extraite (extraite de la suite 1/n²(sin(n)), c'est à dire en gardant uniquement certains termes on construit une autre suite) dont la valeur des termes reste assez grande (même quand n est très grand, ce qu'on prouve avec le théorème de Dirichlet), ce qui prouve que la suite ne converge pas vers 0 (et donc, qu'elle ne converge pas du tout, car elle ne peut converger que vers 0 - chose qu'on peut aisément démontrer en construisant une autre suite extraite qui converge vers 0 car sin est dense sur l'intervalle [-1, 1]).

Ce dernier passage est relativement compliqué et pas assez détaillé, mais ce n'est pas grave, l'auteur du topic-boucle ne le comprendra pas non plus.

Voilà les kheys, vous pourrez désormais répondre fièrement à la question boucle : Non, elle ne converge pas.

converge

ce mot est excitant

Le 17 octobre 2022 à 17:57:51 :
Démonstration facile, même un BCPST pour la sortir.
Maintenant Riemann te choppe par le cou et te demande de démontrer la convergence de la série de terme général 1/n^2.sin(n).
Quelle est ta reac-fils-de-hapiste ?

D après le post de l auteur la réponse est non car la suite ne converge pas vers 0

Le 17 octobre 2022 à 17:54:56 :
Il nous laisse partir si on lui répond ça ?

À partir de :
"Une suite converge si elle se rapproche toujours plus d'un certain nombre"

Il te gifle avec un Dunod et t'interdis de lui adresser la parole/de le regarder/ de te trouver dans la même pièce que lui avant que tu ai appris tes définitions.