Un khey chaud en maths?

Le 20 juin 2022 à 22:02:16 :
+1

Le 20 juin 2022 à 22:07:32 :
Écris le produit scalaire de p par Du sous forme de somme, et tu verras que le sup sous |p(i,j)| <= 1 est précisément F(u) (maximise chaque terme de la somme de façon indépendante)

c'est ce que j'ai essayé, mais je n'y arrive pas

Le 20 juin 2022 à 22:09:44 :

Le 20 juin 2022 à 22:07:32 :
Écris le produit scalaire de p par Du sous forme de somme, et tu verras que le sup sous |p(i,j)| <= 1 est précisément F(u) (maximise chaque terme de la somme de façon indépendante)

c'est ce que j'ai essayé, mais je n'y arrive pas

Quelle est la définition de la norme |.| sur Y ?

Le 20 juin 2022 à 22:13:36 :

Le 20 juin 2022 à 22:09:44 :

Le 20 juin 2022 à 22:07:32 :
Écris le produit scalaire de p par Du sous forme de somme, et tu verras que le sup sous |p(i,j)| <= 1 est précisément F(u) (maximise chaque terme de la somme de façon indépendante)

c'est ce que j'ai essayé, mais je n'y arrive pas

Quelle est la définition de la norme |.| sur Y ?

norme euclidienne

Maximise chaque coordonnée de façon indépendante, dans la suite on va donc se concentrer sur la maximisation de p1 * Du1 + p2 * Du2, sous la contrainte que |p| <= 1.

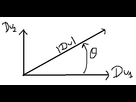
Si tu considères le problème dans un plan (Du1 vecteur horizontal et Du2 vertical), trace la somme de ces deux vecteurs. Sa norme est précisément |Du|, et tu l'obtient en prenant p1 = cos(theta) et p2 = sin(theta). p respecte bien la contrainte, et c'est bien évidemment le sup.

Le 20 juin 2022 à 22:24:17 :
Maximise chaque coordonnée de façon indépendante, dans la suite on va donc se concentrer sur la maximisation de p1 * Du1 + p2 * Du2, sous la contrainte que |p| <= 1.

Si tu considères le problème dans un plan (Du1 vecteur horizontal et Du2 vertical), trace la somme de ces deux vecteurs. Sa norme est précisément |Du|, et tu l'obtient en prenant p1 = cos(theta) et p2 = sin(theta). p respecte bien la contrainte, et c'est bien évidemment le sup.

j'ai pas compris, mais merci je réessayerais demain

Le 20 juin 2022 à 22:35:12 :

Le 20 juin 2022 à 22:24:17 :
Maximise chaque coordonnée de façon indépendante, dans la suite on va donc se concentrer sur la maximisation de p1 * Du1 + p2 * Du2, sous la contrainte que |p| <= 1.

Si tu considères le problème dans un plan (Du1 vecteur horizontal et Du2 vertical), trace la somme de ces deux vecteurs. Sa norme est précisément |Du|, et tu l'obtient en prenant p1 = cos(theta) et p2 = sin(theta). p respecte bien la contrainte, et c'est bien évidemment le sup.

j'ai pas compris, mais merci je réessayerais demain

Ouais je suis claqué donc j'explique mal et j'ai sans doute dû faire qques petites erreurs, mais je pense que c'est l'idée

Le 20 juin 2022 à 22:24:17 :
Maximise chaque coordonnée de façon indépendante, dans la suite on va donc se concentrer sur la maximisation de p1 * Du1 + p2 * Du2, sous la contrainte que |p| <= 1.

Si tu considères le problème dans un plan (Du1 vecteur horizontal et Du2 vertical), trace la somme de ces deux vecteurs. Sa norme est précisément |Du|, et tu l'obtient en prenant p1 = cos(theta) et p2 = sin(theta). p respecte bien la contrainte, et c'est bien évidemment le sup.

• On se concentre sur une seule coordonnée (i,j), donc on note pour plus de clarté p=p(i,j) et Du=Du(i,j)

Ça doit être plus clair comme ça déjà