[MATHS] J'ai une QUESTION à propos des SONDAGES

On parle souvent de la marge d'erreur dans les sondages, cependant il y a un truc qui me paraît évident :
si un candidat est donné à 0%, il ne peut pas y avoir une marge d'erreur de 2%. Sinon ça lui est forcément favorable étant donné qu'il ne peut pas être en score négatif.

Par exemple, sur ce tableau d'Harris Interractive :

Les marges d'erreur dépendent du score du candidat.

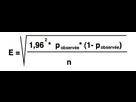
Du coup, voici ma question : comment calcule-t-on la marge d'erreur en fonction du score ? Car tous les sites que je trouve donnent une marge d'erreur fixe. En fait, je voudrais trouver la marge d'erreur pour un candidat qui fait 1% par exemple. Merci !

PS : c'est pas pour l'école Jean-J'aide pas

question intéressante

Le 23 février 2022 à 21:07:58 :
Je suis une grosse kiche en math dsl

C'est pas grave, merci pour le up

Je comprend pas où est ton problème la marge d'erreur signifie que la vraie valeur V0 se situe entre V±m ça signifie que:
V0 € [V-m;V+m] si le V= 0 ça signifie que V0€[0;V+m] étant donné qu'on sait qu'elle n'est pas négative, ce qui nous permet de raccourcir l'intervalle de confiance.

En gros un intervalle de confiance statistique n'est pas forcément centré et symétrique comme on a l'habitude, d'ailleurs ya aucune raison à cela

Le 23 février 2022 à 21:15:59 :
Je comprend pas où est ton problème la marge d'erreur signifie que la vraie valeur V0 se situe entre V±m ça signifie que:
V0 € [V-m;V+m] si le V= 0 ça signifie que V0€[0;V+m] étant donné qu'on sait qu'elle n'est pas négative, ce qui nous permet de raccourcir l'intervalle de confiance.

En gros un intervalle de confiance statistique n'est pas forcément centré et symétrique comme on a l'habitude, d'ailleurs ya aucune raison à cela

Alors pourquoi des tableaux existent ?

Le 23 février 2022 à 21:20:24 :

Le 23 février 2022 à 21:15:59 :
Je comprend pas où est ton problème la marge d'erreur signifie que la vraie valeur V0 se situe entre V±m ça signifie que:
V0 € [V-m;V+m] si le V= 0 ça signifie que V0€[0;V+m] étant donné qu'on sait qu'elle n'est pas négative, ce qui nous permet de raccourcir l'intervalle de confiance.

En gros un intervalle de confiance statistique n'est pas forcément centré et symétrique comme on a l'habitude, d'ailleurs ya aucune raison à cela

Alors pourquoi des tableaux existent ?

Khey va falloir développer un peu plus là

La tableau dont tu as fait le screen donne selon la taille de ton échantillon et selon la certitude que tu veux avoir sur ta donnée la marge d'erreur que tu dois prendre en compte.

Quand tu prend un échantillon tu calcules les résultats du sondage pour un candidat et autour de chaque valeur tu crées un intervalle centré sur la valeur qui plus il sera large plus il sera "fiable" (au sens de comprendra la réelle valeur qu'on cherche)

C'est bon, j'ai trouvé. Pour un échantillon de n personnes, et pour un pourcentage trouvé p, la marge d'erreur à 95% est :

Interprétation : si un candidat fait un score p dans un sondage, il y a 95% de chances qu'il se situe dans [p-E ; p+E].

Remarque : pour 99%, utiliser 2,58 au lieu de 1,96

Le 23 février 2022 à 21:28:34 :
La tableau dont tu as fait le screen donne selon la taille de ton échantillon et selon la certitude que tu veux avoir sur ta donnée la marge d'erreur que tu dois prendre en compte.

Quand tu prend un échantillon tu calcules les résultats du sondage pour un candidat et autour de chaque valeur tu crées un intervalle centré sur la valeur qui plus il sera large plus il sera "fiable" (au sens de comprendra la réelle valeur qu'on cherche)

Non, toutes les valeurs du tableau sont pour une certitude à 95%. J'ai trouvé ce que je cherchais (voir au-dessus), j'ai vérifié la formule et ça marche sur toutes les valeurs du tableau. Et pour 0%, ça donne bien évidemment un intervalle réduit à un point : 0. Il reste toujours les 5% de chances d'être hors de l'intervalle, mais sur 2000 personnes les chances sont faibles.

Y'a un mec ( je connais plus son nom) qui à calculé comment calculer la marge d'erreur en fonction du nombre de personnes interrogée et la population totale en question et du coup les médias se servent de cet algorithme pour faire la marge d'erreur j'ai pas les détails mais ça se trouve facilement sur internet.

et pour le mec à 0% ça veut dire qu'il à autant de chance de faire 0% ou 2%, on sait pas s'il est réellement à 0% les sondages ne sont qu'un outils de propagande, il ne faut pas l'oublier