Besoin de GENIES en MATHS
- 1
(x,y,z) appartient à F est équivalent à x - 5z = 0 et y=y donc équivalent à x=5z et y=y
Donc une base est donnée par les vecteurs (5, 0, 1) et (0, 1, 0)
On en déduit la dimension
Le 08 décembre 2021 à 21:38:51 :
x - 5z = 0 équivalent à x=5z et y=yDonc une base est donnée par les vecteurs (5, 0, 1) et (0, 1, 0)
On en déduit la dimension
Merci grandement khey 
La dimension c'est 2 si j'ai bien compris ?
Le 08 décembre 2021 à 21:40:47 :
Le 08 décembre 2021 à 21:38:51 :
x - 5z = 0 équivalent à x=5z et y=yDonc une base est donnée par les vecteurs (5, 0, 1) et (0, 1, 0)
On en déduit la dimensionMerci grandement khey
La dimension c'est 2 si j'ai bien compris ?
C'est ça, la dimension d'un espace est égal au nombre d'éléments d'une base de cet espace
Le 08 décembre 2021 à 21:41:38 :
Le 08 décembre 2021 à 21:40:47 :
Le 08 décembre 2021 à 21:38:51 :
x - 5z = 0 équivalent à x=5z et y=yDonc une base est donnée par les vecteurs (5, 0, 1) et (0, 1, 0)
On en déduit la dimensionMerci grandement khey
La dimension c'est 2 si j'ai bien compris ?
C'est ça, la dimension d'un espace est égal au nombre d'éléments d'une base de cet espace
D'accord merci khey 
Pour être tout à fait rigoureux, il faut montrer que (5, 0, 1) et (0, 1, 0) est une famille libre, mais c'est "normalement" évident.
Le 08 décembre 2021 à 21:47:55 :
Je connais pas les exigences de tes profs, je précise que mon raisonnement montre que (5, 0, 1) et (0, 1, 0) est une famille génératrice de F.
Pour être tout à fait rigoureux, il faut montrer que (5, 0, 1) et (0, 1, 0) est une famille libre, je te laisse t'en convaincre.
Ca devrait aller, au pire je perdrais un peu de point si je ne montre pas ça mais ce n'est pas grave.
Le 08 décembre 2021 à 21:54:35 :
Le 08 décembre 2021 à 21:47:55 :
Je connais pas les exigences de tes profs, je précise que mon raisonnement montre que (5, 0, 1) et (0, 1, 0) est une famille génératrice de F.
Pour être tout à fait rigoureux, il faut montrer que (5, 0, 1) et (0, 1, 0) est une famille libre, je te laisse t'en convaincre.Ca devrait aller, au pire je perdrais un peu de point si je ne montre pas ça mais ce n'est pas grave.
Pour deux vecteurs, dis juste qu'ils sont non colinéaires. Pas besoin de justification, c'est voyant ici.
Le 08 décembre 2021 à 21:55:22 :
waaaaa les souvenirs de prépa
Je suis en école d'ingé issou, le problème c'est que j'ai fais BTS --> école d'ingé sans passer par la prépa. Tu te doutes bien qu'en BTS le niveau est abyssal, je ne savais même pas c'était quoi un espace vectoriel il y a deux semaines. 
Le 08 décembre 2021 à 21:56:07 :
Le 08 décembre 2021 à 21:54:35 :
Le 08 décembre 2021 à 21:47:55 :
Je connais pas les exigences de tes profs, je précise que mon raisonnement montre que (5, 0, 1) et (0, 1, 0) est une famille génératrice de F.
Pour être tout à fait rigoureux, il faut montrer que (5, 0, 1) et (0, 1, 0) est une famille libre, je te laisse t'en convaincre.Ca devrait aller, au pire je perdrais un peu de point si je ne montre pas ça mais ce n'est pas grave.
Pour deux vecteurs, dis juste qu'ils sont non colinéaires. Pas besoin de justification, c'est voyant ici.
D'accord merci de l'astuce khey 

- 1
Données du topic
- Auteur
- GohanCalvo
- Date de création
- 8 décembre 2021 à 20:34:28
- Nb. messages archivés
- 15
- Nb. messages JVC
- 15
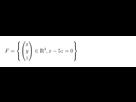

.gif)