[Math/info] Les ingélites venez ici

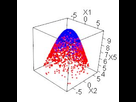
Je dois trouver un moyen de séparer ce jeu de donnée avec une seule et unique droite, pour l'instant c'est impossible car la classe rouge est encerclée par la classe bleu

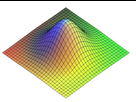
Je cherche une fonction [-6,6] * [-6,6] -------> R telle que plus les points sont au centre (0,0) plus cette fonction a une grande valeur

ça donnera quelque chose comme ça:

vous pensez à quelle type de fonction ?

On dirait que t'as obtenus tes points avec Acos(r) et Bsin(r) ou quelque chose du genre

Essaye X1² + X2²

Quand tu as ça tu vois bien que la frontière séparatrice est pas linéaire

M'enfn y'a un énorme overlap entre les deux classes ça semble difficile

Le 16 novembre 2021 à 15:03:42 :
Quand tu as ça tu vois bien que la frontière séparatrice est pas linéaire

M'enfn y'a un énorme overlap entre les deux classes ça semble difficile

Oui mais le but c'est de projeter X1 et X2 à l'aide d'une application pour justement avoir une frontière linéaire

j'ai eu ça du coup avec la fonction gausienne (10 exp(-x1²/2*6² - x2²/2*6²)

On a une frontière linéaire selon X5

Le 16 novembre 2021 à 15:07:45 :

Le 16 novembre 2021 à 15:03:42 :
Quand tu as ça tu vois bien que la frontière séparatrice est pas linéaire

M'enfn y'a un énorme overlap entre les deux classes ça semble difficile

Oui mais le but c'est de projeter X1 et X2 à l'aide d'une application pour justement avoir une frontière linéaire

j'ai eu ça du coup avec la fonction gausienne (10 exp(-x1²/2*6² - x2²/2*6²)

On a une frontière linéaire selon X5

Ah ok tu utilises une machine à vecteur de support
Mais dans ce cas on a déjà du te parler de fonction noyau ?

Le 16 novembre 2021 à 15:11:50 :

Le 16 novembre 2021 à 15:07:45 :

Le 16 novembre 2021 à 15:03:42 :
Quand tu as ça tu vois bien que la frontière séparatrice est pas linéaire

M'enfn y'a un énorme overlap entre les deux classes ça semble difficile

Oui mais le but c'est de projeter X1 et X2 à l'aide d'une application pour justement avoir une frontière linéaire

j'ai eu ça du coup avec la fonction gausienne (10 exp(-x1²/2*6² - x2²/2*6²)

On a une frontière linéaire selon X5

Ah ok tu utilises une machine à vecteur de support
Mais dans ce cas on a déjà du te parler de fonction noyau ?

Oui mais on a pas le droit de s'en servir Je connais un peu le cours à l'avance mais pour l'instant on ne peut utiliser de SVM, on le verra plus tard, pour l'instant on doit le faire à la main pour utiliser une analyse discriminante linéaire

Le 16 novembre 2021 à 15:12:43 :

Le 16 novembre 2021 à 15:11:50 :

Le 16 novembre 2021 à 15:07:45 :

Le 16 novembre 2021 à 15:03:42 :
Quand tu as ça tu vois bien que la frontière séparatrice est pas linéaire

M'enfn y'a un énorme overlap entre les deux classes ça semble difficile

Oui mais le but c'est de projeter X1 et X2 à l'aide d'une application pour justement avoir une frontière linéaire

j'ai eu ça du coup avec la fonction gausienne (10 exp(-x1²/2*6² - x2²/2*6²)

On a une frontière linéaire selon X5

Ah ok tu utilises une machine à vecteur de support
Mais dans ce cas on a déjà du te parler de fonction noyau ?

Oui mais on a pas le droit de s'en servir Je connais un peu le cours à l'avance mais pour l'instant on ne peut utiliser de SVM, on le verra plus tard, pour l'instant on doit le faire à la main pour utiliser une analyse discriminante linéaire

Tu peux aussi faire une regression linéaire en utilisant x^2,y^2 comme features au lieu de x,y . Ca te permettra de fitter une ellipse de façon relativement simple.

Le 16 novembre 2021 à 13:58:18 :

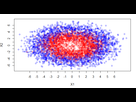
Je dois trouver un moyen de séparer ce jeu de donnée avec une seule et unique droite, pour l'instant c'est impossible car la classe rouge est encerclée par la classe bleu

Je cherche une fonction [-6,6] * [-6,6] -------> R telle que plus les points sont au centre (0,0) plus cette fonction a une grande valeur

ça donnera quelque chose comme ça:

vous pensez à quelle type de fonction ?

Google SVM kernel trick...