les PROFS du FORUM VENEZ TOUS ici !

Le 19 juin 2021 à 22:06:36 :
Je pense à devenir prof juste pour avoir une aventure comme ça ou alors aider un enfant en difficulté à croire en lui et le sauver de la misère (après la question c'est faire prof de quoi et est-ce que je vais tenir en Meef parce que ça à l'air super chiant)

Essaie d'aller dans un lycée prestigieux kheyou.

Les chances d'avoir une aventure comme ça sont dix fois plus grosses.
Quand ils aura son prix nobel et qu'il te remerciera tu aura le même sentiment que un mec qui grimpe l'Everest.

Le 19 juin 2021 à 22:06:10 :

Le 19 juin 2021 à 22:03:53 Rayyn33 a écrit :

Le 19 juin 2021 à 21:53:28 :
- On dispose de 9 poires qui ont toutes exactement le meme poids sauf une un peu plus lourde que les autres.
- On dispose d'une balance parfaitement équilibrée

Quel est le nombre minimal de pesées à effectuer pour identifer à coup sur la poire la plus lourde ? ( Expliquer )

On en pèse 8 divisées en 2 groupes de 4
Si les deux groupes font le même poids la poire laissée de côté est la plus lourde
Sinon on prend le groupe le plus lourd et on réitère le processus en comparant le poids de 2 groupes de deux poires
Le groupe le plus lourd contient la poire la plus lourde et une troisième pesée nous permet de l’identifier

Trop long, on peut le faire en deux pesées. Mais l'esprit est là, réfléchis, ca va te sembler évident

j'ai c'est bon
tu prends
3 +3
si meme poids

si même poids tu pèses les 3 restantes
comme suit 1.5 et 1.5 ( tu la coupes en 2

si poids différents tu prends le plus lourd avec 1.5 et 1.5

si meme poids la poire coupée est la plus lourde sinon c'est le coté qui penche

Le 19 juin 2021 à 22:08:41 MrRiemann a écrit :

Le 19 juin 2021 à 22:06:36 :
Je pense à devenir prof juste pour avoir une aventure comme ça ou alors aider un enfant en difficulté à croire en lui et le sauver de la misère (après la question c'est faire prof de quoi et est-ce que je vais tenir en Meef parce que ça à l'air super chiant)

Essaie d'aller dans un lycée prestigieux kheyou.

Les chances d'avoir une aventure comme ça sont dix fois plus grosses.
Quand ils aura son prix nobel et qu'il te remerciera tu aura le même sentiment que un mec qui grimpe l'Everest.

Ya parfois 100 personnes/jour qui grimpent l'Everest en saison, c'est limite si on te presse pas une fois au sommet pour que tu dégages car t'empêche les autres de monter, et ya des embouteillages de cordée, des insultes des bagarres parfois, sans parler des déchets laissés par les alpinistes

Ah et c'est 50 000 dollars le permis de monter

Le 19 juin 2021 à 22:06:10 :

Le 19 juin 2021 à 22:03:53 Rayyn33 a écrit :

Le 19 juin 2021 à 21:53:28 :
- On dispose de 9 poires qui ont toutes exactement le meme poids sauf une un peu plus lourde que les autres.
- On dispose d'une balance parfaitement équilibrée

Quel est le nombre minimal de pesées à effectuer pour identifer à coup sur la poire la plus lourde ? ( Expliquer )

On en pèse 8 divisées en 2 groupes de 4
Si les deux groupes font le même poids la poire laissée de côté est la plus lourde
Sinon on prend le groupe le plus lourd et on réitère le processus en comparant le poids de 2 groupes de deux poires
Le groupe le plus lourd contient la poire la plus lourde et une troisième pesée nous permet de l’identifier

Trop long, on peut le faire en deux pesées. Mais l'esprit est là, réfléchis, ca va te sembler évident

Ah bah oui suffit de diviser en trois groupes, une pesée suffit à déterminer quel groupe est le plus lourd (soit celui qui n’est pas mis sur la balance en cas d’équilibre soit celui qui est pesé plus lourd qu’un autre) et peser 2 des poires du groupe en question suffit par le même mécanisme (soit on a directement la bonne poire soit c’est celle de côté)

Le 19 juin 2021 à 22:11:48 :

Le 19 juin 2021 à 22:06:10 :

Le 19 juin 2021 à 22:03:53 Rayyn33 a écrit :

Le 19 juin 2021 à 21:53:28 :
- On dispose de 9 poires qui ont toutes exactement le meme poids sauf une un peu plus lourde que les autres.
- On dispose d'une balance parfaitement équilibrée

Quel est le nombre minimal de pesées à effectuer pour identifer à coup sur la poire la plus lourde ? ( Expliquer )

On en pèse 8 divisées en 2 groupes de 4
Si les deux groupes font le même poids la poire laissée de côté est la plus lourde
Sinon on prend le groupe le plus lourd et on réitère le processus en comparant le poids de 2 groupes de deux poires
Le groupe le plus lourd contient la poire la plus lourde et une troisième pesée nous permet de l’identifier

Trop long, on peut le faire en deux pesées. Mais l'esprit est là, réfléchis, ca va te sembler évident

Ah bah oui suffit de diviser en trois groupes, une pesée suffit à déterminer quel groupe est le plus lourd (soit celui qui n’est pas mis sur la balance en cas d’équilibré soit celui qui est pesé plus lourd qu’un autre) et peser 2 des poires du groupes en question suffit par le même mécanisme (soit on a directement la bonne poire soit c’est celle de côté)

c'est tellement évident je voulais les découper

Le 19 juin 2021 à 22:11:48 Rayyn33 a écrit :

Le 19 juin 2021 à 22:06:10 :

Le 19 juin 2021 à 22:03:53 Rayyn33 a écrit :

Le 19 juin 2021 à 21:53:28 :
- On dispose de 9 poires qui ont toutes exactement le meme poids sauf une un peu plus lourde que les autres.
- On dispose d'une balance parfaitement équilibrée

Quel est le nombre minimal de pesées à effectuer pour identifer à coup sur la poire la plus lourde ? ( Expliquer )

On en pèse 8 divisées en 2 groupes de 4
Si les deux groupes font le même poids la poire laissée de côté est la plus lourde
Sinon on prend le groupe le plus lourd et on réitère le processus en comparant le poids de 2 groupes de deux poires
Le groupe le plus lourd contient la poire la plus lourde et une troisième pesée nous permet de l’identifier

Trop long, on peut le faire en deux pesées. Mais l'esprit est là, réfléchis, ca va te sembler évident

Ah bah oui suffit de diviser en trois groupes, une pesée suffit à déterminer quel groupe est le plus lourd (soit celui qui n’est pas mis sur la balance en cas d’équilibré soit celui qui est pesé plus lourd qu’un autre) et peser 2 des poires du groupes en question suffit par le même mécanisme (soit on a directement la bonne poire soit c’est celle de côté)

Exactement

Le 19 juin 2021 à 22:13:43 linterlope3 a écrit :

Le 19 juin 2021 à 22:11:48 :

Le 19 juin 2021 à 22:06:10 :

Le 19 juin 2021 à 22:03:53 Rayyn33 a écrit :

Le 19 juin 2021 à 21:53:28 :
- On dispose de 9 poires qui ont toutes exactement le meme poids sauf une un peu plus lourde que les autres.
- On dispose d'une balance parfaitement équilibrée

Quel est le nombre minimal de pesées à effectuer pour identifer à coup sur la poire la plus lourde ? ( Expliquer )

On en pèse 8 divisées en 2 groupes de 4
Si les deux groupes font le même poids la poire laissée de côté est la plus lourde
Sinon on prend le groupe le plus lourd et on réitère le processus en comparant le poids de 2 groupes de deux poires
Le groupe le plus lourd contient la poire la plus lourde et une troisième pesée nous permet de l’identifier

Trop long, on peut le faire en deux pesées. Mais l'esprit est là, réfléchis, ca va te sembler évident

Ah bah oui suffit de diviser en trois groupes, une pesée suffit à déterminer quel groupe est le plus lourd (soit celui qui n’est pas mis sur la balance en cas d’équilibré soit celui qui est pesé plus lourd qu’un autre) et peser 2 des poires du groupes en question suffit par le même mécanisme (soit on a directement la bonne poire soit c’est celle de côté)

c'est tellement évident je voulais les découper

J'ai explosé à ton "explication"

Le 19 juin 2021 à 22:13:43 :

Le 19 juin 2021 à 22:11:48 :

Le 19 juin 2021 à 22:06:10 :

Le 19 juin 2021 à 22:03:53 Rayyn33 a écrit :

Le 19 juin 2021 à 21:53:28 :
- On dispose de 9 poires qui ont toutes exactement le meme poids sauf une un peu plus lourde que les autres.
- On dispose d'une balance parfaitement équilibrée

Quel est le nombre minimal de pesées à effectuer pour identifer à coup sur la poire la plus lourde ? ( Expliquer )

On en pèse 8 divisées en 2 groupes de 4
Si les deux groupes font le même poids la poire laissée de côté est la plus lourde
Sinon on prend le groupe le plus lourd et on réitère le processus en comparant le poids de 2 groupes de deux poires
Le groupe le plus lourd contient la poire la plus lourde et une troisième pesée nous permet de l’identifier

Trop long, on peut le faire en deux pesées. Mais l'esprit est là, réfléchis, ca va te sembler évident

Ah bah oui suffit de diviser en trois groupes, une pesée suffit à déterminer quel groupe est le plus lourd (soit celui qui n’est pas mis sur la balance en cas d’équilibré soit celui qui est pesé plus lourd qu’un autre) et peser 2 des poires du groupes en question suffit par le même mécanisme (soit on a directement la bonne poire soit c’est celle de côté)

c'est tellement évident je voulais les découper

effectivement j’y ai pensé aussi au début mais c’est beaucoup plus simple que ça

Considérons deux carrés de coté 2 ayant le meme centre

Expliquer pourquoi l'aire de leur intersection est plus grande que 3

Le 19 juin 2021 à 21:26:06 :
Vous connaissez Gauss ?
L'un des plus grands génies que la terre ait porté et pourtant ses deux parents étaient illettrées.
Sa mère ne se souvenait même pas de sa date de naissance.

Pourtant gauss avait un brillant talent pour les mathématiques.

Un de ses professeurs, un certain J.G. Büttner décèle chez Gauss son don des mathématiques et s'efforce de le traiter différemment de ses camarades ; ainsi, en 1786, il fait acheminer depuis Hambourg plusieurs manuels d'arithmétique bien spécifiques, à ses propres frais. Il encadre le jeune Gauss tout au long du cycle élémentaire. Il lui apprend à lire correctement, lui enseigne la grammaire et l'orthographe du haut allemand standard, avec lequel Gauss n'était guère familiarisé, sa langue natale étant le bas allemand. Il l'oblige à soigner son écriture et il est le premier à affiner son immense talent en mathématiques.

Alors voilà ma question ? Avez vous déjà eu un élève extrêmement brillant, un élève que vous êtes sûr de voir réussir ? Et le cas échéant allez vous vous comportez de la même manière que J.G Büttner ?

Dans le second cas si il réussit vous seriez d'autant plus responsable.

Non

Le 19 juin 2021 à 22:08:41 :

Le 19 juin 2021 à 22:06:36 :
Je pense à devenir prof juste pour avoir une aventure comme ça ou alors aider un enfant en difficulté à croire en lui et le sauver de la misère (après la question c'est faire prof de quoi et est-ce que je vais tenir en Meef parce que ça à l'air super chiant)

Essaie d'aller dans un lycée prestigieux kheyou.

Les chances d'avoir une aventure comme ça sont dix fois plus grosses.
Quand ils aura son prix nobel et qu'il te remerciera tu aura le même sentiment que un mec qui grimpe l'Everest.

Je pense pas avoir le niveau et honnêtement si j'arrive à "sauver" des enfants de milieu populaire de toute propagande et trajectoire sociale mauvaise ça me rendra heureux aussi.

J'hésite vraiment à go prof le salaire me fait peur + je ne sais pas si je fais Meef Ses ou Meef eco-gestion

Le 19 juin 2021 à 22:18:30 :
Considérons deux carrés de coté 2 ayant le meme centre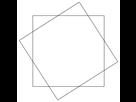

Expliquer pourquoi l'aire de leur intersection est plus grande que 3

Jviens de voir ton énigme, je crois avoir trouvé c’est assez simple
La distance la plus courte pour aller du centre à un point d’un carré est de 2/2 donc 1 quelque soit le carré
Donc on peut imaginer un cercle de rayon 1 dont l’aire sera inférieure à l’aire de l’intersection des deux carrés
En découle ce qu’il fallait expliquer, l’aire sera donc forcément supérieure à pi

Le 19 juin 2021 à 22:48:45 :

Le 19 juin 2021 à 22:18:30 :
Considérons deux carrés de coté 2 ayant le meme centre

Expliquer pourquoi l'aire de leur intersection est plus grande que 3

Jviens de voir ton énigme, je crois avoir trouvé c’est assez simple
La distance la plus courte pour aller du centre à un point d’un carré est de 2/2 donc 1 quelque soit le carré
Donc on peut imaginer un cercle de rayon 1 dont l’aire sera inférieure à l’aire de l’intersection des deux carrés
En découle ce qu’il fallait expliquer, l’aire sera donc forcément supérieure à pi

aya ma technique

Le 19 juin 2021 à 22:56:52 :

Le 19 juin 2021 à 22:48:45 :

Le 19 juin 2021 à 22:18:30 :
Considérons deux carrés de coté 2 ayant le meme centre

Expliquer pourquoi l'aire de leur intersection est plus grande que 3

Jviens de voir ton énigme, je crois avoir trouvé c’est assez simple
La distance la plus courte pour aller du centre à un point d’un carré est de 2/2 donc 1 quelque soit le carré
Donc on peut imaginer un cercle de rayon 1 dont l’aire sera inférieure à l’aire de l’intersection des deux carrés
En découle ce qu’il fallait expliquer, l’aire sera donc forcément supérieure à pi

aya ma technique

j’ai mis plus de temps à comprendre ton écriture qu’à résoudre l’énigme
Mais je crois que ta technique marche que dans un cas particulier non? la question c’est quelle que soit l’orientation des carrés

Le 19 juin 2021 à 22:48:45 Rayyn33 a écrit :

Le 19 juin 2021 à 22:18:30 :
Considérons deux carrés de coté 2 ayant le meme centre

Expliquer pourquoi l'aire de leur intersection est plus grande que 3

Jviens de voir ton énigme, je crois avoir trouvé c’est assez simple
La distance la plus courte pour aller du centre à un point d’un carré est de 2/2 donc 1 quelque soit le carré
Donc on peut imaginer un cercle de rayon 1 dont l’aire sera inférieure à l’aire de l’intersection des deux carrés
En découle ce qu’il fallait expliquer, l’aire sera donc forcément supérieure à pi

Ouaip, bien joué