[MATH] La COHÉRENCE des MATHÉMATIQUES :rire:

Le 03 juin 2021 à 13:07:42 :

Le 03 juin 2021 à 13:05:50 :

[13:04:21] <Quarksbold>

Une explication les mathix ?

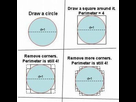
Le périmètre a pas de raison de converger vers la circonférence du cercle, ici c'est une convergence plus faible que ça

Pourtant 3.14 est pas mal éloigné de 4

Justement, je te dis que ça s'en approche pas et que ça n'a rien de paradoxal

Le 03 juin 2021 à 13:08:45 :

Le 03 juin 2021 à 13:06:21 :

Le 03 juin 2021 à 13:04:21 :

Une explication les mathix ?

Tu veux qu'on t'explique quoi ? Que périmètre et surface c'est deux choses différentes ?

Chut le mec pense que le périmètre correspond à l'aire

Vous avez rien compris mais paz

Le 03 juin 2021 à 13:04:21 :

Une explication les mathix ?

Il y a une explication mathématique, mais ça requiert des connaissances poussées, pour faire simple, le périmètre de la limite n'est pas égale à la limite du périmètre

Le 03 juin 2021 à 13:08:45 :

Le 03 juin 2021 à 13:06:21 :

Le 03 juin 2021 à 13:04:21 :

Une explication les mathix ?

Tu veux qu'on t'explique quoi ? Que périmètre et surface c'est deux choses différentes ?

Chut le mec pense que le périmètre correspond à l'aire

T'es sous substances kheyou ?

On pose P=X^2 +1

P n'a pas de racines un carre est jamais négatif.

Posons i = X barre (X avec la barre au dessus)

Alors P(i)=0

NORMAL

Le 03 juin 2021 à 13:09:47 :

Le 03 juin 2021 à 13:04:21 :

Une explication les mathix ?

Il y a une explication mathématique, mais ça requiert des connaissances poussées, pour faire simple, le périmètre de la limite n'est pas égale à la limite du périmètre

Ça me va

Le 03 juin 2021 à 12:53:06 :
J'ai un gateau, je le divise en 0 morceau = je le touche pas = il reste 1 morceau = impossible selon les maths

Autre incohérence : les entiers = comptage, les négatifs = reculer, les nombres réels = mesurer, les nombres imaginaires = nombres qui n'existent pas

Et sinon, l'infini est quelque chose de sans fin, 0 est le milieu de l'infini, quelque chose de sans fin a un milieu

Divise ton gateau en 0,1, tu comprendras peut être
Les nombres imaginaires existent, ils sont nés pour répondre à des opérations impossibles dans R
Imagine un élastique que tu étends des deux côtés, tu arrives à trouver son milieu même si sa distance augmente infiniment (en supposant la résistance absolue)

Je feed mais tu pourras close ton topic la low IQ

Le 03 juin 2021 à 13:10:37 :
On pose P=X^2 +1

P n'a pas de racines un carre est jamais négatif.

Posons i = X barre (X avec la barre au dessus)

Alors P(i)=0

NORMAL

Y'a une faute dans ton postulat de base
C'est un carré réel qui n'est jamais négatif, sinon coté imaginaire, i²=-1

Le 03 juin 2021 à 13:07:04 Raghenfred a écrit :

Le 03 juin 2021 à 13:04:21 :

Une explication les mathix ?

Le fait de considérer une ligne courbe comme une suite de ligne brisée est une approximation incorrecte
Prends un fil et fait un cercle de 1cm de diamètre avec et regarde si le fil utilisé fait 3 ou 4 cm si t'es pas convaincu

La longueur d'une courbe est définie comme une limite de longueur de lignes brisées.
Ce qui fait qu'on a l'impression d'avoir un paradoxe, c'est que la convergence de cette ligne brisée vers le cercle est trop simple. Pour passer à la limite dans les longueurs, on doit demander une convergence beaucoup plus forte (au sens de la variation totale).

Le 03 juin 2021 à 13:04:21 :

Une explication les mathix ?

Pi=4

Le 03 juin 2021 à 13:10:37 PrepaMaths a écrit :
On pose P=X^2 +1

P n'a pas de racines un carre est jamais négatif.

Posons i = X barre (X avec la barre au dessus)

Alors P(i)=0

NORMAL

Modulo P évidemment