[MATHS] help pour un dm sur les matrices
Le 06 mai 2021 à 19:06:09 :
Le 06 mai 2021 à 19:02:07 :
Le 06 mai 2021 à 18:58:51 :
Le 06 mai 2021 à 18:57:31 :
j'ai trouvé une relation de reccurence mais j'arrive pas a la demontrer
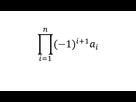
non kheyou je retrouve bien -240 avec cette formule
C'est vrai mais je vais te détailler mon raisonnement par construction mtn que j'ai commencé

Le 06 mai 2021 à 19:02:07 :
Le 06 mai 2021 à 18:58:51 :
Le 06 mai 2021 à 18:57:31 :
j'ai trouvé une relation de reccurence mais j'arrive pas a la demontrer
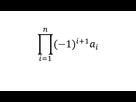
non kheyou je retrouve bien -240 avec cette formule
n pair : Dans un premier temps le produit de -a1 jusqu'à -a(n-2) en faisant le det par bloc sur la première ligne. Le nombre de moins est pair (car il y a (n-2) -1 et (n-2) est pair) donc ça revient à dire le produit de a1 jusqu'à a(n-2). Puis on finit avec le det de
0 a(n-1)
an 0
Soit -1*a(n-1)*an. Donc le det au final vaut -1*a1*...*an
n impair : Dans un premier temps le produit de a1 jusqu'à a(n-2) en faisant le det par bloc sur la première ligne. (Cette fois ci pas de moins au préalable). Puis on finit avec le det de
0 a(n-1)
an 0
Soit -1*a(n-1)*an. Donc le det au final vaut -1*a1*...*an aussi

Le 06 mai 2021 à 19:09:33 :
Le 06 mai 2021 à 19:02:07 :
Le 06 mai 2021 à 18:58:51 :
Le 06 mai 2021 à 18:57:31 :
j'ai trouvé une relation de reccurence mais j'arrive pas a la demontrer
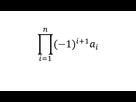
non kheyou je retrouve bien -240 avec cette formule
n pair : Dans un premier temps le produit de -a1 jusqu'à -a(n-2) en faisant le det par bloc sur la première ligne. Le nombre de moins est pair (car il y a (n-2) -1 et (n-2) est pair) donc ça revient à dire le produit de a1 jusqu'à a(n-2). Puis on finit avec le det de
0 a(n-1)
an 0
Soit -1*a(n-1)*an. Donc le det au final vaut -1*a1*...*an
n impair : Dans un premier temps le produit de a1 jusqu'à a(n-2) en faisant le det par bloc sur la première ligne. (Cette fois ci pas de moins au préalable). Puis on finit avec le det de
0 a(n-1)
an 0
Soit -1*a(n-1)*an. Donc le det au final vaut -1*a1*...*an aussi

il y aurait pas un probleme khey, si tous les coefficients sont positif on aurait un determinant negatif or sur une matrcie random j'ai un det positif
0 0 0 2
0 0 6 0
0 13 0 0
9 0 0 0
Le 06 mai 2021 à 19:20:34 :
Le 06 mai 2021 à 19:09:33 :
Le 06 mai 2021 à 19:02:07 :
Le 06 mai 2021 à 18:58:51 :
Le 06 mai 2021 à 18:57:31 :
j'ai trouvé une relation de reccurence mais j'arrive pas a la demontrer
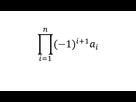
non kheyou je retrouve bien -240 avec cette formule
n pair : Dans un premier temps le produit de -a1 jusqu'à -a(n-2) en faisant le det par bloc sur la première ligne. Le nombre de moins est pair (car il y a (n-2) -1 et (n-2) est pair) donc ça revient à dire le produit de a1 jusqu'à a(n-2). Puis on finit avec le det de
0 a(n-1)
an 0
Soit -1*a(n-1)*an. Donc le det au final vaut -1*a1*...*an
n impair : Dans un premier temps le produit de a1 jusqu'à a(n-2) en faisant le det par bloc sur la première ligne. (Cette fois ci pas de moins au préalable). Puis on finit avec le det de
0 a(n-1)
an 0
Soit -1*a(n-1)*an. Donc le det au final vaut -1*a1*...*an aussi

il y aurait pas un probleme khey, si tous les coefficients sont positif on aurait un determinant negatif or sur une matrcie random j'ai un det positif
0 0 0 2
0 0 6 0
0 13 0 0
9 0 0 0
-2*-6*(-1)*13*9 ? Non ? 
Pour être plus précis mais ça change rien 
Le 06 mai 2021 à 19:22:19 :
Le 06 mai 2021 à 19:20:34 :
Le 06 mai 2021 à 19:09:33 :
Le 06 mai 2021 à 19:02:07 :
Le 06 mai 2021 à 18:58:51 :
Le 06 mai 2021 à 18:57:31 :
j'ai trouvé une relation de reccurence mais j'arrive pas a la demontrer
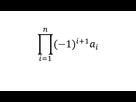
non kheyou je retrouve bien -240 avec cette formule
n pair : Dans un premier temps le produit de -a1 jusqu'à -a(n-2) en faisant le det par bloc sur la première ligne. Le nombre de moins est pair (car il y a (n-2) -1 et (n-2) est pair) donc ça revient à dire le produit de a1 jusqu'à a(n-2). Puis on finit avec le det de
0 a(n-1)
an 0
Soit -1*a(n-1)*an. Donc le det au final vaut -1*a1*...*an
n impair : Dans un premier temps le produit de a1 jusqu'à a(n-2) en faisant le det par bloc sur la première ligne. (Cette fois ci pas de moins au préalable). Puis on finit avec le det de
0 a(n-1)
an 0
Soit -1*a(n-1)*an. Donc le det au final vaut -1*a1*...*an aussi

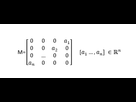
il y aurait pas un probleme khey, si tous les coefficients sont positif on aurait un determinant negatif or sur une matrcie random j'ai un det positif
0 0 0 2
0 0 6 0
0 13 0 0
9 0 0 0-2*-6*(-1)*13*9 ? Non ?

Pour être plus précis mais ça change rien
la calculatrice est formelle khey c'est bien +1404 
Le 06 mai 2021 à 19:25:05 :
Le 06 mai 2021 à 19:22:19 :
Le 06 mai 2021 à 19:20:34 :
Le 06 mai 2021 à 19:09:33 :
Le 06 mai 2021 à 19:02:07 :
Le 06 mai 2021 à 18:58:51 :
Le 06 mai 2021 à 18:57:31 :
j'ai trouvé une relation de reccurence mais j'arrive pas a la demontrer
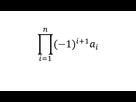
non kheyou je retrouve bien -240 avec cette formule
n pair : Dans un premier temps le produit de -a1 jusqu'à -a(n-2) en faisant le det par bloc sur la première ligne. Le nombre de moins est pair (car il y a (n-2) -1 et (n-2) est pair) donc ça revient à dire le produit de a1 jusqu'à a(n-2). Puis on finit avec le det de
0 a(n-1)
an 0
Soit -1*a(n-1)*an. Donc le det au final vaut -1*a1*...*an
n impair : Dans un premier temps le produit de a1 jusqu'à a(n-2) en faisant le det par bloc sur la première ligne. (Cette fois ci pas de moins au préalable). Puis on finit avec le det de
0 a(n-1)
an 0
Soit -1*a(n-1)*an. Donc le det au final vaut -1*a1*...*an aussi

il y aurait pas un probleme khey, si tous les coefficients sont positif on aurait un determinant negatif or sur une matrcie random j'ai un det positif
0 0 0 2
0 0 6 0
0 13 0 0
9 0 0 0-2*-6*(-1)*13*9 ? Non ?

Pour être plus précis mais ça change rien
la calculatrice est formelle khey c'est bien +1404
Ça semble être positif pour les multiples de 4 seulement, je comprends pas pourquoi 
Mince alors 
n=1
.gif) positif
positifn=2
.gif) négatif
négatifn=3
.gif) négatif
négatifn=4
.gif) positif
positifn=5
.gif) positif
positifn=6
.gif) négatif
négatifn=7
.gif) négatif
négatifn=8
.gif) positif
positifDonnées du topic
- Auteur
- Blacked-equerre
- Date de création
- 6 mai 2021 à 18:44:28
- Nb. messages archivés
- 33
- Nb. messages JVC
- 32


.gif)



