" Tu es INTELLIGENT ? " " Oui, on nous enseigne bien les MATHÉMATIQUES à l'école"

Le 07 avril 2021 à 19:24:21 Okalyptu a écrit :

Le 07 avril 2021 à 19:19:02 Kher- a écrit :

Le 07 avril 2021 à 19:17:15 SoldatGaulois a écrit :

Le 07 avril 2021 à 19:14:38 Kher- a écrit :
Une droite c'est soit 2 points soit 1 point et une pente l'ahuri
Avec la tangente t'as un point et une pente

La pente est déterminée par un deuxième point

Non

Si c'est vrai, l'analyse est assez simple, la droite dont l'auteur veut parler c'est l'approximation affine f(a) ~ f'(a)(x-a) + f(a), l'expression de la pente f'(a) contient bien deux points, infiniment proche

Cependant l'auteur ne prouve rien du tout et rend les choses encore plus confuse

Non y'a pas deux points infiniment proches y'a juste la limite d'une valeur qui est le taux d'accroissement, une droite c'est un point et une pente ou deux points et la tangente est définie par un point (le point tangent) et une pente qui est la valeur de la dérivée en ce point.

Le 07 avril 2021 à 19:28:45 KheyKholleur a écrit :

Le 07 avril 2021 à 19:24:21 Okalyptu a écrit :

Le 07 avril 2021 à 19:19:02 Kher- a écrit :

Le 07 avril 2021 à 19:17:15 SoldatGaulois a écrit :

Le 07 avril 2021 à 19:14:38 Kher- a écrit :
Une droite c'est soit 2 points soit 1 point et une pente l'ahuri
Avec la tangente t'as un point et une pente

La pente est déterminée par un deuxième point

Non

Si c'est vrai, l'analyse est assez simple, la droite dont l'auteur veut parler c'est l'approximation affine f(a) ~ f'(a)(x-a) + f(a), l'expression de la pente f'(a) contient bien deux points, infiniment proche

Cependant l'auteur ne prouve rien du tout et rend les choses encore plus confuse

"Deux points infiniment proches"
Vous en êtes restés aux conceptions mathématiques du 17e siècle avec les infiniment petits... Ça fait bien longtemps que plus personne ne fait ça comme ça en mathématiques.

Que tu le veuille ou non, il s'agit bien de deux points distincts, sinon la dérivée n'a pas de sens

Maintenant tu peux rester sur ce sujet débattre pendant dix ans et refuser d'avoir tord, moi je me casse

Le 07 avril 2021 à 18:32:36 AlfredLeI a écrit :

Le 07 avril 2021 à 18:23:20 SoldatGaulois70 a écrit :

La dérivée, la courbe magique qui passe par un seul point

Sans lire ton exemple tu dis vrai, c'est horrible la red pill que l'on se prend en prépa scientifique lorsque le prof te dit cash "vous avez appris que de la merde auparavant", pour ensuite voir au fur et à mesure que c'est vrai

J'en ai rien à foutre de l'opax et son bordel, mais par contre cette choucroute en signature, mon bon khey

Le 07 avril 2021 à 19:31:56 Okalyptu a écrit :

Le 07 avril 2021 à 19:28:45 KheyKholleur a écrit :

Le 07 avril 2021 à 19:24:21 Okalyptu a écrit :

Le 07 avril 2021 à 19:19:02 Kher- a écrit :

Le 07 avril 2021 à 19:17:15 SoldatGaulois a écrit :

Le 07 avril 2021 à 19:14:38 Kher- a écrit :
Une droite c'est soit 2 points soit 1 point et une pente l'ahuri
Avec la tangente t'as un point et une pente

La pente est déterminée par un deuxième point

Non

Si c'est vrai, l'analyse est assez simple, la droite dont l'auteur veut parler c'est l'approximation affine f(a) ~ f'(a)(x-a) + f(a), l'expression de la pente f'(a) contient bien deux points, infiniment proche

Cependant l'auteur ne prouve rien du tout et rend les choses encore plus confuse

"Deux points infiniment proches"
Vous en êtes restés aux conceptions mathématiques du 17e siècle avec les infiniment petits... Ça fait bien longtemps que plus personne ne fait ça comme ça en mathématiques.

Que tu le veuille ou non, il s'agit bien de deux points distincts, sinon la dérivée n'a pas de sens

Maintenant tu peux rester sur ce sujet débattre pendant dix ans et refuser d'avoir tord, moi je me casse

Déjà khey tu confond dérivée et tangente qui sont deux objets différents alors fait pas trop le malin

Le 07 avril 2021 à 19:31:56 Okalyptu a écrit :

Le 07 avril 2021 à 19:28:45 KheyKholleur a écrit :

Le 07 avril 2021 à 19:24:21 Okalyptu a écrit :

Le 07 avril 2021 à 19:19:02 Kher- a écrit :

Le 07 avril 2021 à 19:17:15 SoldatGaulois a écrit :

Le 07 avril 2021 à 19:14:38 Kher- a écrit :
Une droite c'est soit 2 points soit 1 point et une pente l'ahuri
Avec la tangente t'as un point et une pente

La pente est déterminée par un deuxième point

Non

Si c'est vrai, l'analyse est assez simple, la droite dont l'auteur veut parler c'est l'approximation affine f(a) ~ f'(a)(x-a) + f(a), l'expression de la pente f'(a) contient bien deux points, infiniment proche

Cependant l'auteur ne prouve rien du tout et rend les choses encore plus confuse

"Deux points infiniment proches"
Vous en êtes restés aux conceptions mathématiques du 17e siècle avec les infiniment petits... Ça fait bien longtemps que plus personne ne fait ça comme ça en mathématiques.

Que tu le veuille ou non, il s'agit bien de deux points distincts, sinon la dérivée n'a pas de sens

Maintenant tu peux rester sur ce sujet débattre pendant dix ans et refuser d'avoir tord, moi je me casse

Paz sur toi le desco qui croit avoir saisi les mathématiques avec un bagage première S

Le 07 avril 2021 à 18:27:12 SoldatGaulois70 a écrit :

Le 07 avril 2021 à 18:26:07 Rammus_fan a écrit :
????? mais j'ai pas les mots, nice troll

Y a 0 troll

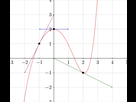
Sur l'image on te montre des tangentes qui passent par UN point sur la courbe.

Or, on ne peut pas tracer une droite à partir d'un seul point

mdr j'ai ri