[MATH/INFO] Vous la comprenez comment cette notation ?

Le 26 janvier 2021 à 01:11:56 AR7CORE a écrit :
Le n^O(1) perso je le lis comme "pour chaque n", juste un truc de liaison, mais je peux me tromper
L'algo doit faire quoi ?

On a un graphe avec n sommets, l'algo doit dire s'il existe un sous-ensemble de k sommets tels que toute arete du graphe est en contact avec au moins l'un de ces sommets.

Mais osef un peu de ce que doit faire mon algo, je veux déjà comprendre la notation
Je pense l'avoir comprise mais j'aimerais juste qu'on confirme / réfute ce que j'ai dit en page précédente

notamment cette affirmation :
"n^O(1)" c'est pareil que "n puissance x, pour une certaine constante x"

Le 26 janvier 2021 à 01:23:13 AR7CORE a écrit :
Tu dois déterminer si le sous graphe existe ou le trouver ?
Si tu dois juste montrer qu'il existe, y'a juste à comparer la branche racine de chaque noeud à considérer, ça marche pour les graphes qui ont qu'un noeud parent.
Si 2 sommets ont pas un noeud en (grand) parent, c'est qu'ils sont situés de part et d'autre du graphe, en remontant la ligne parentale, plus tu dois remonter pour retomber sur un noeud en commun, plus les nœuds de départ sont éloignés, si le seul ancêtre commun c'est la racine du graphe lui même c'est qu'il y a pas de sous graphes strictement plus petit qui les contiennent.
Tu peux considérer le graphe comme un sous-ensemble de lui même ? Si oui, return true, complexité constante 😁

Oui c'est gentil, merci ! Et effectivement on doit juste dire si ça existe, sans le trouver; Mais je m'en fiche de l'algorithme, je l'ai déjà

Je veux juste comprendre la notation 2^k * n^O(1)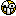
Actuellement j'ai déjà le famoso algorithme mais je dois comprendre si oui ou non il a la bonne durée.

Je sais que l'algo que j'ai a une durée de O(2^k * polynome(n))(je n'ai pas + d'info sur la gueule du polynome pour l'instant), et je voudrais savoir la différence entre ça et " 2^k * n^O(1) "

Le 26 janvier 2021 à 01:26:55 AR7CORE a écrit :
Non truc^O(machin) c'est pas un calcul à faire, ici "machin" est déjà un résultat, c'est une mesure, avec pas la même unité que ce qui est sans le polynômes, je persiste à dire que la puissance c'est juste pour lier les 2 composantes, une simple notation

Alors là je ne comprends pas ce que tu dis
Je ne comprenais déjà pas ton post de bas de page 1

"""
Je sais que l'algo que j'ai a une durée de O(2^k * polynome(n))(je n'ai pas + d'info sur la gueule du polynome pour l'instant), et je voudrais savoir la différence entre ça et " 2^k * n^O(1) "
"""

La différence c'est que dans le premier cas, le nombre de calculs dépend du polynôme de n et dans le deuxième cas il dépend de n.
Pour un truc de notation aussi spécifique faudrait voir avec celui qui t'a donné l'énoncé, j'ai un doute sur ce que ça voudrait dire pour lui.

Le 26 janvier 2021 à 00:49:08 Questiondinfo a écrit :

Le 26 janvier 2021 à 00:47:32 TheLelouch4 a écrit :
O(1) c'est juste une quantité bornée qui est indépendante de n, pour dire que c'est un truc constant en le nombre d'opérations

Ok merci pour la réponse!
Donc ça peut vraiment se lire "n puissance x pour une certaine constante x" ?

Oui.
edit : tout les exemples que t'as donné sont dans ces temps.

UP !

Le 26 janvier 2021 à 01:42:18 MusicIsMath a écrit :

Le 26 janvier 2021 à 00:49:08 Questiondinfo a écrit :

Le 26 janvier 2021 à 00:47:32 TheLelouch4 a écrit :
O(1) c'est juste une quantité bornée qui est indépendante de n, pour dire que c'est un truc constant en le nombre d'opérations

Ok merci pour la réponse!
Donc ça peut vraiment se lire "n puissance x pour une certaine constante x" ?

Oui.
edit : tout les exemples que t'as donné sont dans ces temps.

Quelqu'un confirme ?