[Maths] La géométrie derrière le jeu du Dobble

Aujourd'hui, en prévision du retour de l'école à la maison suite au renforcement du confinement probable le mois prochain, j'ai décidé d'éduquer un peu la masse inculte que vous êtes en vous présentant des maths que vous ne verrez pas au lycée.

On va donc utiliser le jeu du Dobble pour parler un peu de géométrie projective finie.

Pour rappel, le Dobble est un jeu de 55 cartes. Chaque carte compte 8 symboles, et chaque paire de carte compte exactement un symbole en commun pour les deux cartes. Si vous êtes un peu curieux, vous avez pu vous demander comment c'est possible, et comme Micmath n'a pas encore fait de vidéo sur le sujet, il se pourrait bien que vous ne le sachiez pas encore.

Si vous suivez un peu, je vais essayer de vous expliquer comment fonctionne le jeu du Dobble, et son lien fondamental avec une géométrie exotique. Vous devriez également comprendre pourquoi le Dobble devrait en fait compter 57 cartes, pourquoi on peu construire un jeu de Dobble avec 6, 8 ou 12 symboles par cartes mais pas avec 7, 9 ou 10. Enfin, vous pourriez même créer votre propre jeu de Dobble. Mais par dessus tout, vous aurez découvert de belles maths et rempli un peu votre caboche avec autre chose que les carabistouilles habituelles de ce lieu de perdition.

Introduction
On va commencer par essayer de comprendre pourquoi je vous parle de géométrie, et quel peut bien être le lien avec des cartes et des symboles. Ça va nous permettre d'illustrer un principe fondamental des maths du XXème (et du XXIème) siècle : on se fout bien de savoir ce que sont les objets que l'on manipule, seules importent les relations qu'ils ont entre eux, c'est à dire leur comportement vis-à-vis les uns des autres.

Je vais donc d'ores et déjà formuler l'analogie séminale de notre tentative de compréhension du Dobble :

Une carte de Dobble correspond à une droite du plan, et un symbole correspond à un point de ce plan. Un symbole figure sur une carte si le point correspondant au symbole appartient à la droite correspondant à la carte.

• Confondues, c'est à dire que ce sont les mêmes.
• Parallèles, c'est à dire qu'elles ne se croisent pas.
• Sécantes, c'est à dire qu'elles se croisent en un seul et ua​ime point.

• Identiques, c'est à dire que ce sont les mêmes
• Sécantes, c'est à dire qu'elles sont un symbole en commun

Exercice : Quel est le symbole en commun dans la paire de carte sur l'image ci-dessus ?
C'est l'araignéent

1. Il existe des droites parallèles alors qu'il n'existe pas de cartes "parallèles"
2. Une droite passe par une infinité de points alors qu'une carte ne compte que 8 symboles.

Eh bien nous allons traiter chacun de ces deux problèmes séparément. Une fois que nous aurons mis en place les outils pour les résoudres, nous aurons créé une géométrie abstraite, qui ne ressemblera plus du tout à la géométrie du monde physique, mais qui décrira parfaitement un jeu de Dobble.

1. La géométrie projective
2. La géométrie finie

I La géométrie projective

Notre but ici, est de régler le problème des droites parallèles : elles doivent disparaître.

1. Retirer des droites de notre géométrie
2. Rajouter des points

Pour qu'il n'y ait plus de droites parallèles entre elles, on pourrait essayer de prendre, pour une droite de référence, toutes les droites parallèles à celle-ci puis toutes les retirer sauf une. Ça marcherait, mais on perdrait beaucoup de droites, et donc beaucoup de cartes possibles dans notre jeu final. Ce serait un petit peu dommage.
Par exemple, on pourrait ne garder que les droites passant par un certain point fixé, et alors on n'aurait plus de droites parallèles entre elles... Seulement toutes nos droites se croiseraient en un même point, et donc toutes nos cartes auraient exactement le même symbole en commun. Pas très intéressant comme jeu, à part peut-être pour une certaine partie du forum.

On va donc se concentrer sur notre seconde option : inventer de nouveaux points. Et pour cela, on va s'inspirer des lois de la perspective :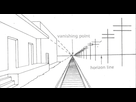
Quand on regarde le dessin ci-dessus, on comprend que les droites représentant les deux côtés des rails sont parallèles. Pourtant, on voit sur le dessins qu'elles se croisent en un point, situé sur la ligne d'horizon. C'est ce que nous appellerons le point à l'infini.

Le point à l'infini est donc un point conceptuel auquel se rejoignent deux droites parallèles. Seulement il nous reste une question à résoudre :
Comben y a-t-il de points à l'infini ? En effet, si toutes les droites passent par point à l'infini, deux droites qui étaient déjà sécantes de base vont maintenant se croiser en deux points distincts : le point où elles se croisaient déjà à la base et le point à l'infini.
Il faut donc que ces deux droites passent par des points à l'infini qui ne sont pas les mêmes.
Pour reprendre notre analogie avec la perspective, imaginez sur le dessin une autre paire de rails allant dans une autre direction. Les deux rails se croiseraient à un point différent de la ligne d'horizon.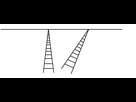

Une fois ces observations faites, il ne nous faut pas beaucoup d'effort pour comprendre de combien de points à l'horizon nous avons besoin : il en faut une infinité, un point pour chaque groupe de droites parallèles entre elles.
Pour les "compter", on peut donc dire que l'on considère un point à l'infini pour chaque droite passant par un certain point d'origine. En effet, deux droites passant par ce point d'origine ne peuvent être parallèles entre elles et toute droite du plan est parallèle à exactement une droite passant par le point d'origine (c'est le fameux 5ème postulat d'Euclide : https://fr.wikipedia.org/wiki/Axiome_des_parall%C3%A8les )

Ainsi nous pouvons reformuler un petit peu notre analogie séminale pour comprendre le Dobble :

Une carte de Dobble correspond à une droite du plan projectif, et un symbole correspond à un point de ce plan. Un symbole figure sur une carte si le point correspondant au symbole appartient à la droite correspondant à la carte.

II La géométrie finie
On va maintenant s'attaquer à résoudre le problème suivant : une droite du plan euclidien classique passe par une infinité de points alors qu'une carte de Dobble ne compte qu'un nombre fini de symboles.

Pour bien comprendre ce qui va se passer ici, il faut comprendre le lien entre les nombres et la géométrie. Ce lien est donné par le concept de coordonnées cartésiennes.

Souvenez-vous donc, au lycée, quand vous parliez d'un point, vous lui donniez des coordonnées (x;y), que vous appelliez abscisse et ordonnée, et qui donnaient la position de ce point dans le plan. C'est exactement ce dont je parle ici.

On va donc commencer par un petit rappel de lycée pour les plus jeunes d'entre vous pour lesquels les smartphones étaient déjà démocratisé quand vous passiez votre brevet et qui ont donc passé leurs cours de maths à poster sur JVC plutôt qu'à écouter leur GÉNIAL prof de maths.

Donc le topo est simple :
Chaque point du plan est représenté par deux nombres, son abscisse et son ordonnée. On les notera (x;y).
Par exemple, si (1;2) sont les coordonnées du point M, il va se retrouver ici sur le plan :
Maintenant, pour représenter un objet géométrique, on peut écrire une équation qui implique x et y.
Par exemple, si je parle de l'objet d'équation 2x + 3y = 5, ça veut dire que je parle de l'objet qui contient tous les points de coordonnées (x;y) telles que l'égalité 2x + 3y = 5 est vérifiée.
Du coup, le point (1,1) va appartenir à cet objet. Et le point (1/2,4/3) également.

En fait, ce que l'on appelle une droite n'est autre qu'un objet avec une équation du style 2x + 3y = 5 ou bien 2.5 x + 9.3 y = 7.

Exercice : À quoi ressemble l'équation d'une droite horizontale ? Et celle d'une droite verticale ?
Une droite horizontale a une équation du type y = 3 et une droite verticale a une équation du type x = 2. Si vous avez mis d'autres nombres à la place de 3 et 2, c'est pas grave.

En général, on appellera équation de droite une équation de la forme 2x + 3y = 4, où l'on peut bien sûr remplacer 2, 3 et 4 par n'importe quel nombre.

Maintenant qu'on a bien compris que la géométrie est liée au système de nombres, on sait ce qu'il nous reste à faire : Inventer un monde où il n'y a qu'une quantité finie de nombres !

Plus précisément, on a besoin d'un système de nombre où il n'y en a qu'une quantité finie, mais on a besoin d'avoir des opérations d'addition, de soustraction, de multiplication et de division qui fonctionne bien, puisque nos équations de droites utilisent ces opérations.

Pour cela, on va utiliser les mathématiques de l'horloge

On va donc s'imaginer une horloge. Pour commencer, on va prendre une horloge classique avec 12 nombres dessus.
La seule différence, c'est qu'on va remplacer le 12 par un 0, mais vous allez voir que c'est juste une histoire de notation.

Donc sur une horloge, on a accès à une douzaine de nombres, et on sait tous comment compter.
0, 1, 2, 3... Et puis on arrive à 10, 11. Et là on a envie de dire 12, mais il n'y est pas. Mais si on continue à tourner, on retombe sur 0 et du coup on boucle.

De même, on peut comprendre assez facilement ce que ça veut dire d'additionner et de soustraire des nombres sur une horloge. S'il est trois heures et que j'attends quatre heures, il sera sept heures : 3 + 4 = 7.
Et puis s'il est sept heures, c'est qu'il y a deux heures il était cinq heures : 7 - 2 = 5
La seule petite subtilité, c'est de voir que par exemple, s'il est onze heures et que j'attends 5 heures, il va être 4 heures sur mon horloge : 11 + 5 = 4.
Une autre manière de comprendre ça, c'est que dans la vraie vie, 11 + 5 = 16. Mais 16 = 12 + 4. Et sur notre horloge, 12, c'est 0. Donc 16 = 4

Maintenant, il va falloir définir la multiplication sur l'horloge.
Si j'attends deux fois cinq heures, j'attends 10 heures. Donc 2 * 5 = 10.
Mais si j'attends, par exemple, deux fois dix heures, ça va faire vingt heures. Et ving n'existe pas sur mon horloge. En fait, en vingt heures, mon horloge va faire une fois le tour (12 heures) puis va avancer de huit heures. Donc 2*10 = 8.

'Exercice : Sur l'horloge, combien font 3*4, 8+7 et 9*5 ?
3*4 = 0, 8+7 = 3 et 9*5 = 9

Bon, maintenant on a l'addition, la soustraction et la multiplication. On va pouvoir passer à la plus compliquée de toutes, la division !

Reprenons notre horloge, et cherchons à réponde à la question suivante : "Il est zéro heures, combien de fois dois-je attendre cinq heures pour qu'il soit dix heures ?"
Eh bien on a dit plus tôt que 2*5 = 10, donc clairement, si j'attends deux fois cinq heures, il sera dix heures !
Autrement dit, 10 divisé par 5 égal 2.

Mais maintenant, mettons qu'il soit zéro heures, et que je veuille attendre par paquets de quatre heures jusqu'à ce que l'aiguille pointe sur neuf. Combien de fois quatre heures dois-je attendre ?

Je peux attendre aussi longtemps que je veux, ça n'arriverai pas. Si j'attends quatre heures l'aiguille affichera quatre. Puis si j'attends encore quatre heures, l'aiguille sera sur le huit. Et si j'attends une troisième fois quatre heures, l'aiguille terminera sur zéro. Et puis ça va recommencer. 4, 8, 0, 4, 8, 0... Impossible de tomber sur 9.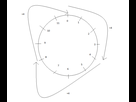

Autrement dit, 4*3 = 0.
Et du coup, il n'est pas vraiment possible, dans le monde de l'horloge, de diviser par 4. Sinon, on aurait 4*3 / 4 = 3 et donc 0 = 3

Eh bien soit ! Le problème vient du fait que 3*4 = 12 (dans la vraie vie). Mais il existe des nombres qui ne poseront pas ce problème... Les nombres premiers
Les nombres premiers, comme 2 3, 5, 7, 11... n'admettent pas d'autres diviseurs que 1 et eux mêmes. Autrement dit, il est impossible d'écrire un truc comme 3*4 = 7. La seule manière d'écrire 7 comme une multiplication avec des nombres entiers, c'est d'écrire 1*7 = 7 ou 7*1 = 7.

Ainsi, si on remplace notre horloge à 12 nombres par une horloge à 7 nombres, on éliminera notre problème et la division fonctionnera correctement dans notre monde.

Nous pouvons donc revenir à notre géométrie. Cette fois-ci, les coordonnées de nos points correspondront à des nombres sur notre horloge à 7 chiffres. On peut voir les choses à peu près comme ça :
Ici, les seuls points qui existent dans notre géométrie sont les points qui se situent sur la grille, à l'intersection d'une ligne verticale et d'une ligne horizontale. De plus, quand on sort de la grille d'un côté, on re-rentre en face, façon Pacman

Voyons encore un exemple : traçons la droite d'équation 2x + y = 1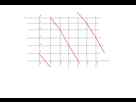

Ainsi, nous allons pouvoir identifier nos cartes de Dobble à nos droites dans un monde où les droites ne passent que par un nombre fini de points.
Il nous reste à combiner ce concept avec le concept de la géométrie projective pour résoudre tous nos problèment.

En attendant, on peut encore préciser notre analogie :

Une carte de Dobble correspond à une droite du plan projectif fini, et un symbole correspond à un point de ce plan. Un symbole figure sur une carte si le point correspondant au symbole appartient à la droite correspondant à la carte.

III La géométrie projective finie

On y est, on a maintenant tous les outils en main pour construire notre Dobble à 8 symboles.

On va partir de notre plan de géométrie finie
Auquel il va falloir rajouter un certain nombre de points à l'infini.
Comme on a dit à la fin de la partie I, il y a un point à l'infini par droite passant par le point d'origine. Des droites comme ça, il y en a 8 possibles :
Une droite pour chaque point de la colonne n°1. En effet, si une droite passant par l’origine n’est pas verticale, elle doit passer par un (et un seul !) point de la colonne n°1. Par exemple, voici la droite passant par l'origine et le deuxième point de la deuxième colonne :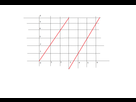
Plus la droite verticale :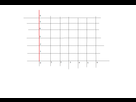

Ça nous fait donc 8 points à l'infini à rajouter à notre plan fini pour obtenir le plan projectif fini :

Et voilà, on n'a plus qu'à choisir un symbole pour chaque point (en n'oubliant pas les points à l'infini) et on peut construire les cartes de notre jeu de Dobble en traçant toutes les droites de notre plan projectif (ce qui demande de s'exercer un peu, je le concède).

Je vous laisse maintenant avec une énigme : Pourquoi devrait-il normalement y avoir 57 cartes dans un jeu de Dobble classique ?
Le premier à trouver la réponse aura la classe. Si vous avez une licence de maths ou plus, laissez chercher vos camarades.

Le 08 novembre 2020 à 15:38:38 LeFameuxAmi a écrit :
Le mec nous recopie sa thèse oklm sur le forum.

Ça aurait pu être ma thèse si j'avais vécu au XIXème siècle.

Le 08 novembre 2020 à 15:41:07 skywear a écrit :

Je recommande de réviser cette présentation, elle pourra faire son petit effet le soir du réveillon après avoir fait une partie de Dobble avec votre tante.

Le 08 novembre 2020 à 15:50:56 Fkeuz a écrit :
Tres intéressant
Combiner plusieurs concepts pour modéliser quelque chose ça se fait assez peu dans le scolaire c'est dommage

Je te rassure cela dit, l'idée ne vient pas de moi. Je pense que les créateurs du Dobble avaient bien en tête ces principes quand ils ont conçu le jeu.

Ça ressemble bien à un délire de matheux, d'ailleurs. De se dire qu'on va faire jouer des gens à trouver le point d'intersection entre deux droites projectives discrètes en remplaçant les concepts géométriques par des cartes ou des dessins.

Le 08 novembre 2020 à 15:59:59 [Jenaimarre2] a écrit :
C'est point de fuite, pas "point à l'infini"

En terme artistique, oui. Mais j'utilise un vocabulaire différent parce que mon but est de parler de mathématiques et de pas trop m'attacher à l'analogie de la perspective.
Cela dit, j'utiliserai peut-être les deux dénomination si je décide de reprendre et d'améliorer le texte. Tu penses que ça rendrait l'explication plus claire ?

Le 08 novembre 2020 à 15:52:34 Dagnyr a écrit :

Le 08 novembre 2020 à 15:50:56 Fkeuz a écrit :
Tres intéressant
Combiner plusieurs concepts pour modéliser quelque chose ça se fait assez peu dans le scolaire c'est dommage

Je te rassure cela dit, l'idée ne vient pas de moi. Je pense que les créateurs du Dobble avaient bien en tête ces principes quand ils ont conçu le jeu.

Ça ressemble bien à un délire de matheux, d'ailleurs. De se dire qu'on va faire jouer des gens à trouver le point d'intersection entre deux droites projectives discrètes en remplaçant les concepts géométriques par des cartes ou des dessins.

C'est un peu perché oui ce qui est fou je trouve c'est qu'on ait besoin d'une démonstration aussi compliquée pour modéliser un truc d'apparence assez simple

Le 08 novembre 2020 à 16:23:13 Punch8Ball a écrit :
Je ne comprends pas pourquoi il n'existe que 8 points à l'infini pour les droites passant par l'origine ?

C'est parce qu'il n'existe que 8 droites passant par l'origine.
Pour voir ça, tu peux te dire que toute droite passant par l'origine est soit verticale, soit oblique/horizontale. Et si elle est oblique ou horizontale, elle passe forcément par un seul point de la deuxième droite verticale. Et cette deuxième droite verticale compte elle même 7 points.
Ça te fait donc 7 droites obliques/horizontale + 1 droite verticale, soit huit droites.